Lupine Publishers | Current Investigations in Agriculture and Current Research
Abstract
We consider a plane steady-state filtration in a rectangular bridge with a partially impermeable vertical wall in the presence of evaporation from a free surface of groundwater. To study the effect of evaporation, a mixed multi parametric boundary-value problem of the theory of analytic functions is formulated and using the method of P. Y. Polubarinova-Kochina. Based on the proposed model, an algorithm is developed to calculate the dependence of efficiency and productivity of hydrodynamic analysis.
Keywords: Filtration; Evaporation; Jumper; Ground water; Free surface; Polubarinova-Kochina method; Complex velocity; Conformal mappings; Differential equations of the Fuchs class
Introduction
As it is known [1-6], the exact solution of tasks on inflow of liquid to an imperfect well with the flooded filter (i.e. an axisymmetric task) or the tubular well representing an impenetrable pipe with the filter in its some part is connected with great mathematical difficulties and so far isn’t found. Therefore in due time as the first approach to the solution of similar tasks some corresponding flat tasks analogs about a filtration to imperfect rectilinear gallery in free-flow layer [4,7] and in a rectangular crossing point with partially impenetrable vertical wall were considered [8]. It should be noted that areas of complex speed of the specified cases allow applying by means of inversion at the decision Christoffel- Schwartz’s formula.
In work [9] it is shown that the current picture near the impenetrable screen significantly depends not only on imperfection of gallery, but also on evaporation existence that is strongly reflected in an expense of gallery and ordinate of a point of an exit of a curve depression to an impenetrable wall.
In the real work the exact analytical solution of a task on a current of ground waters through a rectangular crossing point with partially impenetrable vertical wall in the presence of evaporation from a free surface of ground waters is given. In this case in the field of complex speed, unlike [1,4,6-8] there are not rectilinear, but circular polygons that doesn’t give the chance to use classical integral of Christoffel-Schwartz. For the solution of a task P.Y. Polubarinova-Kochina’s method is used [1-6]. By means of developed for areas of a special look [10-12] which are characteristic for problems of an underground hydromechanics, ways of conformal display of circular polygons [13-19] decides mixed multiple parameter tasks of the theory of analytical functions. The accounting of characteristics of the considered current allows to receive the decision through elementary functions that does its use by the simply and convenient. The provided detailed hydrodynamic analysis gives the flavor about possible dependence of filtration characteristics of the movement on all physical parameters. The received results, at least, qualitatively can be postponed for a case of tubular wells.
Formulation of the Problem
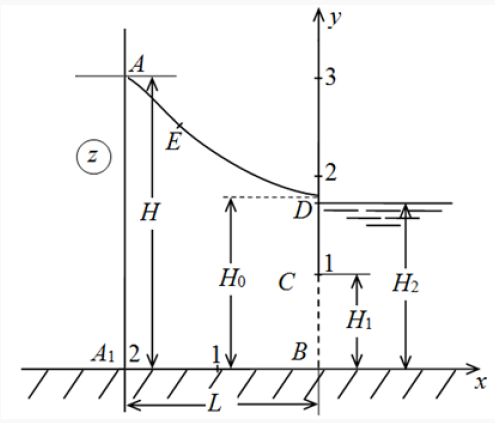
In Figure 1 the rectangular crossing point with slopes of AA1 and DB on the impenetrable horizontal basis of length of L is presented. Water height in the top tail of Н, lower tail with water level of Н2, having partially impenetrable vertical wall CD (screen), adjoins a layer sole. If the working part of the crossing point CB (filter) of width of H1 is flooded, H2>H1, an interval of seepage, usual for dams, is absent [1]. The upper bound of area of the movement is the free surface of AD, coming to the disproportionate CD, screen to which there is a uniform evaporation of intensity ε(0<ε<). Soil is considered uniform and isotropic, the current of liquid submits to Darci law with known coefficient of a filtration κ=const.
We will enter the complex potential of the movement ω =ϕ + iψ ( φ–speed potential, ψ–function of current) and complex coordinates z = x + iy , carried respectively κH and H, where H – a pressure in A point. At choice of system of coordinates specified Figure 1 and at combination of the plane of comparison of pressures with the y=0 plane on border of area of a filtration the following regional conditions are satisfied:
The task consists in definition of provision of a free surface of AD and finding of ordinate of H0 – points of an exit of a curve depression to the impenetrable screen, and also a filtration expense of Q.
Creation of the Decision
For the solution of a task we use P Y Polubarinova-Kochina’s method which is based on application of the analytical theory of the linear differential equations of a class of Fuchs [1-6,20]. We will enter: auxiliary area t–semi-strip Ret >0, 0<Imt < 0.5π a parametrical variable t at compliance of points tA =∞, 1 1 0.5 , 0.5 A B t = arcth a + π t = arcth b + π i (1<a1<b<∞), a1, b – unknown affixes of points A1 and B in the plane , 0.5 C t t = π i and 0 D t = ; function z(t), conformally displaying a plane t semi-strip on area z, and also derivative dω/dt и dz/dt. We will address to area of complex speed of w, corresponding to boundary conditions (1) which is represented a circular quadrangle of ACDE with a section with top in E point (the corresponding inflection point of a curve depression) and a corner Πν = 2arctg ε at A, top belongs to a class of polygons in polar grids and was investigated [12-19] earlier. It is important to emphasize that similar areas, despite the private look, however are very typical and characteristic for many problems of an underground hydromechanics: at a filtration from channels, sprinklers and reservoirs, at currents of fresh waters over based salty, in problems of a flow of the tongue of Zhukovsky in the presence of salty retaining waters (see, for example, [9,21]).
The function making conformal display of a semi-strip to area of complex speed of w, has a former appearance [9]
Where С (C ≠ 1) – some suitable material constant.
Defining characteristic indicators of the dω/dt and dz/dt functions about regular special points [1-6, 20], considering that w=dω/dz and in view of a ratio (2), we will come to dependences
Where М>0 – a large-scale constant of modeling.
It is possible to check that functions (3) meet the boundary conditions (1) reformulated in terms of the dω/dt и dz/dt, functions and, thus, are the parametrical solution of an initial regional task. Record of representations (3) for different sites of border of a semistrip with the subsequent integration on all contours of auxiliary area of the parametrical t leads to short circuit of area of a current and, thereby, serves as control of calculations.
As a result we receive expressions for the set sizes: width of the L crossing point, water level in the top H and the lower H2 the tail`s and lengths of H1 of the filter
and also required coordinates of points of a free surface AD
and expressions for a filtrational expense of Q and ordinate of a point of an exit of a free surface to the screen
Control of the account are other expressions for sizes Q, H0 and L
directly following from boundary conditions (1).
In formulas (4)-(10) sub integral functions–expressions of the right parts of equalities (3) on the corresponding sites of a contour of auxiliary area t. Limit case. At merge of points of A and A1, in the plane t, at a1→1 (arcth a1=∞) the crossing point degenerates in freeflow layer semi-infinite at the left and the task about a current of ground waters to imperfect gallery investigated earlier [9] turns out.
Calculation of the Scheme of A Current and Analysis of Numerical Results
Representations (3)–(10) contain four unknown constants of M, C, a1 and b. The parameters a1, b (1< a1<b<∞), C (C ≠ 1) are defined from the equations (4) for the set sizes H1,H2 (H1≤H2<H) and L, constant modeling of M thus is from the second equation (4), fixing water level H in the top tail of a crossing point. After definition of unknown constants consistently there is a filtration expense of Q ordinate of H0 of a point of an exit of a curve depression to an impenetrable site DC on formulas (6) and coordinates of points of a free surface of DA on formulas (5). In Figure 1 the current picture calculated at ε=0.5 , H=3, L=2, H1=1.0, H2=1.4 (basic option [9]) is represented. Results of calculations of influence of the defining physical parameters ε, H, H1, H2 and L at sizes Q and H0 are given in Tables 1 & 2. In Figure 2 dependences of an expense of Q (curves 1) and ordinates H0 of an exit of a curve depression to the screen (curves 2) from parameters ε, H, H1, H2 and L. Рис.2 Dependences of the sizes Q and H0 from ε (а) at H=3, L=2, H1=1 H2=1.4, , from H (б) at ε=0.5, L=2, H1=1, H2=1.4; от L(в) at ε=0.5, H=3, H1=1, H2=1.4; from H1 (г) at ε=0.5, H=3, L=2, H2=1.4; from H2(д) при ε=0.5, H=3, L=2, H1=1.
Figure 2: Dependences of the sizes Q and H0 from ε(а) at H=3, L=2, H1=1 H2=1.4, from H(б) at ε=0.5, L=2, H1=1, H2=1.4; от L (в) at ε=0.5, H=3, H1=1, H2=1.4; from H1(г) at ε=0.5, H=3, L=2, H2=1.4; from H2 (д) при ε=0.5, H=3, L=2, H1=1.
The analysis of these tables and schedules allows drawing the following conclusions. First of all opposite qualitative nature of change of the sizes Q and H0 at a variation of parameters attracts attention ε, H and L (Table 1): also, as well as earlier [9] reduction ε and increase H is led to increase of an expense and ordinates of an exit of a curve depression to the screen. Thus, in relation to a filtration in a crossing point reduction of intensity and evaporation plays the same role, as well as increase in a pressure. Thus the greatest influence on the sizes Q and H0 renders a pressure: at increase of parameter H by only 1.2 times the expense and ordinate increase more, than 52 and 24% respectively. Essential interest is represented by dependences of an expense of a crossing point and ordinate of a point of an exit of a free surface to the screen from water level of H2 in the lower tail, and also from extent of deepening of the screen, i.e. from the size H1 at fixed ε, H and L (Table 2). Here as well as concerning parameters ε and H observed opposite qualitative nature of change of the sizes Q and H0 at a variation of H1 and H2. It is visible that increase in water level of H2 in the lower tail and reduction of deepening of the H1 screen are followed by reduction of an expense and raising of a free surface that, in turn, it is expressed in increase in H0; both of these factors characterize strengthening a sub time.
Follows from Table 1 and Figure 2 that reduction of the H1 и H2 parameters respectively at 1.45 and 1.29 times attracts change of size Q for 16.8 % (at fixation of H1) and 12 % (at fixation of H2). Noted regularities lead to the conclusion that the expense of a crossing point depends on the size of lowering of the level in a little bigger degree, than on filter length (or from imperfection of a well or a well). From Figure 2 it is visible that for basic option almost all dependences of the sizes Q and H0 on parameters ε, H, H1, H2 and L are close to the linear. Comparison of the results received for basic option Q=1.155 and H0=1.776 with results Q=1.141 and H0=1.768 for basic option [9] where the current area was limited equipotential at the left shows that the relative error is very small and makes only 0.5 and 1.3% respectively.
Comparison of value of the expense Q=1.16, received for basic option to Q=1.26, value which follows at application of the generalized I.A. Charny’s formula [1, with. 267] for a usual rectangular crossing point (without screen) in the presence of evaporation leads 8.3% to an error.
For comparison with results [7] we will consider option ε=0.1, H=1, L=4, H1=0.05, H2=0.238 for which Q=42, H0=0.75 is received, and, therefore, relative errors make respectively 71 and 61%. Thus, as well as in [9], here too evaporation significantly influences a current picture.
Conclusion
The technique of creation of the exact analytical solution of a task on the movement in liquid in a rectangular crossing point with the screen in the presence of evaporation from a free surface of ground waters is developed. It is shown that the current picture near the impenetrable screen significantly depends not only on the filter size, but also on evaporation existence that is strongly reflected in an expense and ordinate of a point of an exit of a curve depression to the screen. The received results give an idea (at least qualitatively) of possible dependence of characteristics of a current by consideration of a task about a filtration already to an imperfect well or a tubular well.
Read More Lupine Publishers Agriculture Journal Articles:

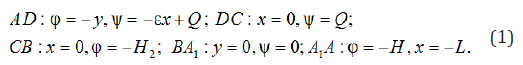
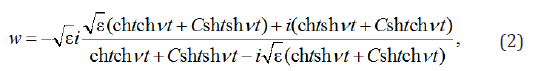
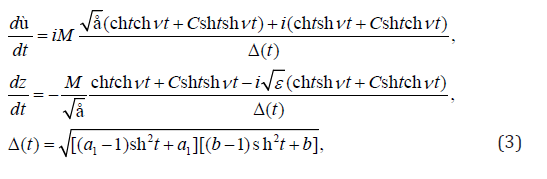
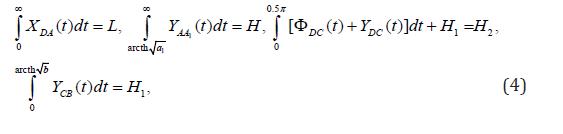
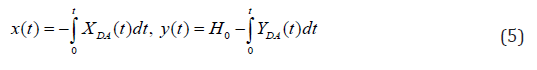
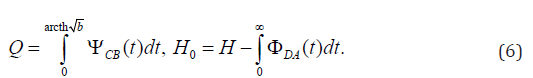
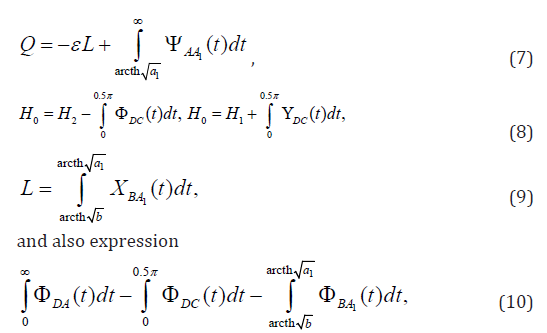


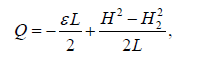
No comments:
Post a Comment
Note: only a member of this blog may post a comment.