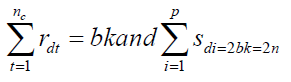Lupine Publishers | Journal of Forensic & Genetic Science
Abstract
In the common sense view, time is the cause of aging. But common sense knows nothing about either one or the other; to the extent that common sense confuses age, aging and old age, breaking all the rules of terminological precision.
Introduction
The concept of Aging
First of all, let's see why aging is a consequence rather than a cause., through three examples:
a) The gradual staining of teeth does not result from aging; instead of that, it's a prodrome of aging.
b) Wrinkles are not the result of aging; they appear when cells have exhausted their ability of scissiparity. We can say that wrinkles are one of causes of aging among others (inter alia)
« Wrinkles (observed reality) « ⇒ aging (concept) »
c) Osteoarthritis is not the result of aging; it results rather from antecedent factors. In fact, aging is a consequence of osteoarthritis:
« Osteoarthritis (observed reality » ⇒ « aging (concept) »
Wrinkles and osteoarthritis are syndromes of aging
Medicine draws a distinction between chronological age, which is expressed with time units, and biological age, which depends on the physical health of an individual, and which is expressed in units of estimated time. For non living things, such as artifacts, we have introduced the expression "technical age".
The Chronological Age
Age, that is chronological age, is a concept of time. It is roughly evaluable, but not observable: no medical expert can accurately guess the exact age of an individual. Strictly speaking, age is a concept corresponding to "what separates birth from today": the relevant information, expressed as a number of years, months, and days, is very poor. Age of all things, alive or not, increases at the same rate. A person who has been around for a great many years is considered aged, something that does not inform in any way as to his or her physical or mental health. The verb "to age" has a double meaning: to become aged (age increase) and to become old (deterioration of physical condition). Early in 2014, a Frenchman almost 103 years old beat his personal cycling record by travelling 26 km in one hour: this was the feat of a man who was "advanced in years" - Cicero would say "grandis natu" Gaffiot [1]- but not old.
The Biological Age
Aging, that is the increase in biological age, is a gradual and unavoidable degradation of the physical condition; biological age concerns the physical condition at a given point in the process of aging. This is a reality which is observable, but which is difficult to evaluate. Indeed, there are countless criteria for assessing aging and old age, and the selection of one of them is necessarily arbitrary and incomplete anyway: the information contained by reality is extremely rich.
Figure 1: Comparing the estimated biological age and the
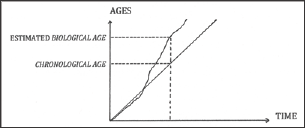
The Figure 1 is an imaginary example: the chronological age curve of an individual is a straight line, while the estimated biological age curve is erratic. On a given date, when the biological age exceeds the chronological age, an individual looks older than the average (Figure 1).
The Technical Age
The "technical age" takes into account the material aging, the wear, the maintenance, as well as the planned obsolescence or not. « Artifact: from Latin « artis factum », made from art. ».
The Aging of Bacteria
Bacteria are prokaryotic unicellular organisms whose genome consists of DNA with one chromosome. The statistical modeling of their development can help.com to understand aging. Bacteria reproduce by splitting through scissiparity one mother turns into two daughters, « ... which in their turn become mothers, each giving two. » daughters, etc. The population doubles with each generation; the exponential increase leads to a mathematical modeling such as:
1 → 2 → 4 → 8 → 16 → 32 → 64 → 128 ... 2 Exp (n)
We start with one bacterium: 1 is written: 2 Exp(0)
The first generation gives 2 bacteria, written: 2 Exp (1)
The second generation gives 4 bacteria, written: 2 Exp(2)
At the nth generation we have N = 2 Exp (n) bacteria
In a homogeneous medium, the generations reproduce at approximately the same rate "μ" (Greek letterμ); therefore, the number "n" of generations is approximately:
n & μ t
where "t" is the time indicated by the laboratory chronometer after "n” duplications. The number of bacteria finally reads:
N # 2Exp (μ t) (1)
The proliferation rate "μ” has three causes:
a) Endogenous factors, specific to the bacterium. They depend on its heredity that is its genotype. One factor is the virulence, defined as the ability to multiply: Escherichia coli are able to divide every 20 minutes. Mbovis (Mycobacterium bovis) has a slower generation rate, but it is just as pathogenic. Benet [2].
b) Exogenous factors, specific to the environmental surrounding: hygrometry, light, temperature, presence of sugar or nitrogen, gravity; for example, salmonella typhimurium is three times more virulent in microgravity.
c) The potentiation of endogenous and exogenous factors, one making the other more effective in some way.
Genotype + surrounding + potentiation ⇒ μ
Temperature is an exogenous factor that is easy to control, and bacteria are very sensitive to temperature: between 20°C and 25°C, a population of Salmonella will double every hour, and within 10 hours, their number will be multiplied by 1000. When the temperature is lowered, the energy intake is reduced and their development is slowed down due to lack of homeothermy: "μ” decreases. Below4°C, the deactivation sets in, and in liquid nitrogen, at c.-196 C (c.77°K), μ = 0.
Homeothermy: Internal regulation of temperature, controlled by the hypothalamus. Dinosaur slacked this function, as do many modern animals, including reptiles.
These experiments have a double interpretation:
a) The rate of proliferation "μ" contains energy components (glucose, heat), hygrometric, gravitational, and chemical components, and possible stochastic factors.
b) Time "t" is not the cause of their development. A "substitution rule” provides a theoretical confirmation: the angle of terrestrial rotation "α” is such as
α =ωt
where "ω” is terrestrial rotation speed. It leads to
t = α / ω
In equation (1) we replace”t” by "α / ω”, and we obtain
N= 2 exp (μ α / ω) (2)
Equation (2) proves that the number of bacteria does not depend on time. Time has no impact on bacteria aging. Work done in the USA has observed non-pathogenic bacteria which are deactivated after about hundred transitions, through exhaustion of their genetic ability of scissi parity prescribed by the genome: this is the clinical death of the line, by completion of a genetic program, without temporal impact. At the 100th generation issued from a primary bacteria, the theoretical population reaches c. 2100 bacteria at time "t100" measured when the duplications, observed with a microscope, stop: then μ = 100 / t100 is the average duplication speed.
From t = 100/n, which is the life expectancy of a bacteria line, and from t100/100, which is the average lifespan of a bacterium, it appears that a favourable environment, by activating vitality (that is the factor "μ”), reduces the life expectancy of a population of bacteria and the average lifespan of a bacterium. Professor Valter Longo, director of the USC School of Gerontology (CA), discovered that bacteria deprived of sugar could double their lifespan. Interesting conclusions can be drawn for human health.
The Aging of Cells
L. Robert refers to the activity of biological clocks in the cell aging process. But the rhythms which are observed are irregular and imprecise, and they depend on the environment: therefore they do not have the reliability and accuracy that a clock should have. The metaphor of the biological arrow of time which is supposed to orient cell development is inappropriate; moreover L. Robert describes interactions between the extracellular matrix and the cell: the cell and the matrix have their own modalities of aging which modify the program sequence of the ECM synthesis and its action on the cell as well Klein. [3] This action, which partly determines mitosis (cell division), finally exhausts its abilities: the author recalls the work done in vitro by L. Hayflick (in the USA in the early 1960s), which has shown a limit of 50 to 60 duplications of the cell population: the analogy with a biological arrow of time is obviously disqualified.
The innocuousness of time is clear from Hayflick conclusions: the life expectancy of a cell depends on the rate of duplication (rate of transtability). Transtability is the ability of a cell, which is unstable like any system, to divide into two cells, themselves unstable, whereupon each new cell then divides in its turn: cytoplasmic division is caused by the quest to reach a steady state which is never in fact achieved. The weaker the transtability, the slower the aging; therefore the aging of a cell can be reduced by acting on main causes of imbalance: stressors and genetic weaknesses. The longevity of a cell is determined by the length of its telomere, which is a segment located at the ends of a chromosome. The telomere gets shorter as the number of cell divisions increases, and also due to stressors. This segment, which is protected by an enzyme (telomerase protects the integrity of the genome), controls the start of mitosis. The telophase, or terminal phase of mitosis, consists in the splitting of the cell nucleus into two nuclei, followed by cell division. Unlike non-pathogenic cells, cancer cells are able to subdivide indefinitely: on a human scale, they do not age, because telomerase is hyperactive inside tumoral cells. A cell does not age because of a biological arrow of time, but because of a genetic and environmental mitogen induction: mitosis is induced by the gene, the environment, and a possible potentiation of these two causes.
The Causes of Aging
Time is not the cause of aging in bacteria and cells. But can this refutation of the confusion between time and aging be generalized to all systems? The innate and the acquired are active components of the aging of any system, living or not: even before it is completed, any building or human-made system begins an aging process: what is innate in a bridge is its architecture, its structure, and the quality of the work and materials; what is acquired derives from functional and climatic stressors, maintenance, and repairs. The anonymous concept of aging is replaced by a more detailed analysis, involving complex engineering and a suitable maintenance protocol.
The Millau Bridge was designed by the English architect Norman Foster for an approximate lifespan of 120 years, which corresponds to 120 terrestrial revolutions. In comparison, the pyramids of Giza are still standing after over 4000 years. They are not simple assemblages of stones: their interior layout includes chambers, passages, and complex anti-intrusion devices. Aging is the normal outcome of the development of living things, regardless of their complexity (ontogeny in humans); it corresponds to a systematic evolution of their state towards different states, resulting from degradation of all their parts, and everything that links and orders these parts. The transtable process. In Latin, trans means beyond (inCaesar); transabeo means go across, go beyond in Virgilius. Gaffiot In the Dictionnaire Larousse 1923, trans means beyond, through. The Dictionnaire Quillet 1929 defines prefix Trans: transition from one state to another.
What is innate in a living being consists essentially of its genetic heritage. The genetic program controls its transtable faculties, as it does inside bacteria and cells. Similar systems age differently from each other, and of course, this would not be the case if time was the cause of their aging. What is acquired is the lifestyle, i.e., the interaction with the rest of the Universe. So a lack of medicalization and hygiene, superimposed on endemic nutritional deficiencies, which generate a range of different pathologies, can reduce life expectancy by a factor of 3 or 4, bringing.com back to the standard of living of the Eneolithic; as shown by the destitution of a billion or so of our fellow humans in the early twenty first century. A report by the Haut Comite de la Sante. Publique [4] gave, for the French male population in 1996, the proportions of deaths due to certain kinds of behaviour relative to the total number of deaths due to all causes: accident 9%, alcohol 13%, tobacco 21% (HCP). The gradual reduction of the gap in average lifespan between men and women which has been observed in recent years is explained by increased smoking and alcohol consumption by women, from adolescence and even pre-adolescence. Data collected in the late 1980s in India showed an inversion of the average lifetimes of men and women: 45 years for men and 43 years for women. (OMS) This reversed gap was explained by the fact that men ate first, while women and children shared the leftovers; in addition, the situation was worsened by smoking among women .The potentiation of reciprocal action between the innate and the acquired constitutes an additional category of active causes of aging (allergies, stressors from different sources, e.g., physical.
Eneolithic: end of Neolithic (3000-2500 BC).
Aging and Organic Degradation
Public access to caves occupied by humans in the paleolithic broke the precarious environmental and atmospheric equilibrium, and triggered a rapid deterioration of petroglyphs by oxidation of pigments and mildew, as observed in the Lascaux caves. In some Egyptian sanctuaries, the same causes brought about the same effects on the magnificent polychromatic frescoes which were found in their original state just before the sanctuaries were opened to crowds of visitors. Museum curators do not consider time to be the cause of aging in the works of art they look after. Light (mainly ultraviolet radiation), temperature, and humidity (and in particular, changes in temperature and humidity), air pollution, inappropriate handling, and specific micro-predators are acknowledged in museum conservation as major aging factors for many materials (wood, leather, paper, textiles, pigments). This is why museums protect their artworks by exposing them only to dim light and ensuring proper ventilation. Very focused efforts are thus made to fight against aging due to physical and chemical stressors, not against the ghostly intervention of time.
The Self Organisation
Belousov's oscillating chemical reactions involve the selforganisation of dissipative structures (Prigogine) [5]. It turns out that these striking experiments are dependent on the necessary supply of fresh reagent: this energy intake modifies the physical state and the organization of the structures. Without it, the reaction would stop. The energy is the sole cause of the observable phenomenon of self-organisation:
No energy ⇒ no self - organization
Therefore, there is no chemical arrow of time in selforganization.
The Biological Arrow Of Time
Spontaneous and extended pulsations of a myocardiac fragment in a glucose solute proceed with the same atemporal protocol; namely, we observe a transtability of the physical state of the fragment, with consumption of energy in the form of sugar. Time is powerless once again:
No energy ⇒ no pulsation
The cardiac pulsations are perfectly observable: a pulsation is not a concept, and the confusion between pulsations and time is obviously a mistake. In addition, the biological rhythms do not comply with the accuracy and regularity requirements of a clock. Therefore, we may talk about biorhythm, but in no way about chronobiology: the biological arrow of time is an inappropriate metaphor.
The Paradox of Aging
These results confirm that aging is not related to time. However, time can be expressed in relation to symptoms of aging of any system, including ourselves:
« Symptoms of aging (observable reality) >⇒» « time goes by »
We conclude with an astonishing paradox, which is summarized by the aphorism:
We don't age because time goes by, but time goes by because we age [6].
Read More About Lupine Publishers Journal of Forensic Sciences Please Click on Below Link:
https://forensic-journal-lupine-publishers.blogspot.com/