Lupine Publishers| Journal of Nanomedicine
Abstract
Energy is an extensive view for industrial advancement. Solar thermal energy is designed by light and heat which is radiated by the sun, in the form of electromagnetic radiation. Solar energy is the highest promptly and sufficiently applicable authority of green energy. Impact of nanoparticle shapes on the Hiemenz nano fluid (water based Cu, Al2O3 and SWCNTs) flow over a porous wedge surface in view of solar radiation energy has been analyzed. The three classical form of nanoparticle shapes are registered into report, i.e. sphere , cylinder and laminar . Nanoparticles in the water based Cu, Al2O3 and SWCNTs have been advanced as a means to boost solar collector energy through explicit absorption of the entering solar energy. The controlling partial differential equations (PDEs) are remodeled into ordinary differential equations (ODEs) by applying dependable accordance alteration and it is determined numerically by executing Runge Kutta Fehlberg method with shooting technique. It is anticipated that the lamina shape SWCNTs have dynamic heat transfer attainments in the flow improvement over a porous wedge surface as compared with the other nanoparticle shapes in different nano fluid flow regime.
Keywords: Nano Particle Shapes, Unsteady Hiemenz Flow, Water Based Cu, Al2O3 and Swcnts, Solar Energy Radiation, Nano Fluids, Solar Thermal Energy, Progressive Technology, Volumetric Receivers, Thermal Attitude
Introduction
Recently nano fluid (water based Cu, Al2O3 and SWCNTs) attracts a noticeable application due to its remarkably energetic heat transfer mechanism. Solar thermal energy is an ideal significant in our regular benefit and it’s a usual system of accessing heat, electricity and water with assist from the nature. As we will address some fossil fuels situation, the solar thermal energy is a sustainable expert of energy which never exhausts. Sustainable energy generation is one of the most important challenges facing society today. Solar thermal energy is one of the principal experts of renewable energy with basic coincidental impact, Sharma et al. [1]. The essential view of ANOAJpting particles to assemble solar energy was analyzed in the 1970s by Hunt [2]. Nanoparticles attempt the possible of developing the radiative assets of liquids, outstanding to enhance in the capability of explicit absorption solar collectors. Heat transfer in the nano fluids (water based Cu, Al2O3 and SWCNTs) due to solar radiation energy is of considerable practical influence to engineers and scientists as a result of its relatively global event in countless units of science and engineering, Choi [3], Buongiorno and Hu [4], Buongiorno [5] and Cheng and Minkowycz [6]. Once again, science and progressive technology is much obliged to solar radiation due to its extensive utilization in the design of solar thermal electricity, solar photovoltaic cells, solar heating, artificial photosynthesis, etc.
Nanoparticle shapes (sphere, cylinder and lamina) in the nano fluids (water based Cu, Al2O3 and SWCNTs) absorb solar radiation notably because of small size as correlated to the wavelength of de Broglie wave. Therefore nanoparticles also attempt the assuring aspect of strengthening the radiative resources of liquids, dominating to accelerate in the performance of straight absorption of solar collectors, [7,8]. Recently, the effects of solar radiation on nano fluid with variable stream conditions were addressed by Das et al. [9] and Anbuchezhian et al. [10].
Many investigators [11-16] have analyzed the utilization of these new transport of heat transfer in solar collectors. Yousefi et al. [11] experimentally presented that the Al2O3/water nanofluid increases the ability of flat-plate collectors by 28.3%. Yousefi et al. [12] studied the effects of pH values of carbon nanotubes nanofluids on the expertise of a flat-plate solar collector. Kameya and Hanamura [13] addressed that the radiation absorption resources of base fluid were increased harmfully by including Ni nanoparticles. Lenert and Wang [14] analyzed the efficiency of nanofluids as volumetric receivers in concentrated solar utilizations applying the suspension of carbon-coated cobalt nanoparticles into Therminol VP-1 fluid. He et al. [15] practically addressed the applicable photo-thermal assets of Cu/H2O nanofluids for enrollment in blunt absorption, solar thermal energy systems.
Furthermore, the up-to-date revision papers [17,18] recorded that nanofluids have strong accessible for utilizations in solar organizations such as solar collectors [19], photovoltaic thermal schemes [20], and thermal energy storage structures [21]. Most of the analysis on the employment of nanofluids in solar collectors has been defined to energy and energy investigations. There are some analyzes on the investigation of the hydrodynamic and convective heat transfer assets of nanofluids in solar structures [16]. As displayed in many review articles [22-24], a massive amount of practical work has been addressed on the thermal attitude of various types of nanofluids flowing through different heat exchanger models; among them, the circular successive tubes have admitted more application in this study since they are the main elemental of various types of solar collectors.
Recently, the capability of applying both nanofluid and porous media has admitted comfortable absorption and has attended to broad analysis in this field. Porous media enhance the association surface area among liquid and solid surface, and, on the other hand, nanoparticles circulated in nanofluid upgrade the impressive thermal conductivity. Therefore, it suggests that utilizing both porous media and nanofluid can enhance the ability of typical thermal systems harmfully. Convective flow in porous media has been universally analyzed in the recent years due to its extensive operations in engineering as post-accidental heat dismissal in solar heater or collectors, drying generating processes, heat exchangers system, geothermal and oil recovery scheme, building construction region, etc. Heat and mass transfer for Hiemenz flow through porous media in the presence of an incident external magnetic field have been studied by several authors [25-30].
The method of Lie group transformations is used to derive all group-invariant similarity solutions of the unsteady twodimensional laminar boundary layer equations, Yurusoy and Pakdemirli [18], Yurusoy and Pakdemirli [19] and Avramenko et al. [31]. Impact of thermal stratification is an important aspect in heat transfer analyses. Thermal stratification of nanofluids occurs due to temperature variations or the presence of different fluids of different densities.
In this article, we addressed the role of nanoparticle shapes (sphere, cylinder and lamina) in the presence of unsteady nanofluids (water based Cu, Al2O3 and SWCNTs) flow and heat transfer past a porous wedge sheet due to solar radiation. Lie symmetry group transformation is applied to transform the controlling PDEs into ODEs and then the numerical solution of the problem is cultivated by using fourth or fifth order Runge Kutta Fehlberg method with shooting technique. Experimental works have analyzed that the nanoparticle shape has a unique impact on the heat and mass transfer of nanofluids [32,33]. Nanoparticle shapes i.e. sphere, cylinder and laminar, are authorized into address in this work. The parameter affirmation for the problem was accomplished and is authorized. It is consumed that the results will gift towards better understanding of nanofluid conflict in channel. Several aspects of the problem are analyzed and predicted graphically with account to the physical parameters elaborated within it and the instant improvements are associated with the applicable literature.
Mathematical Analysis
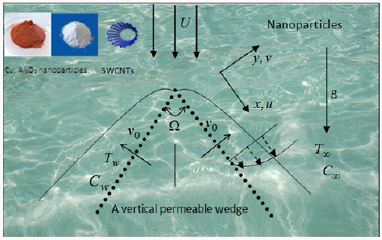
Consider the unsteady laminar two-dimensional flow of an incompressible viscous nanofluids (water based Cu, Al2O3 and SWCNTs) past a porous wedge sheet in the presence of solar energy radiation (Figure 1). The porous medium is assumed to be transparent and in thermal equilibrium with the fluid and neglecting the pressure gradient in the y direction. Due to heating of the entrancing nanofluid and the wedge surface by solar thermal radiation, heat is transmitted from the plate. Also, the solar radiation is a collimated beam that is normal to the plate. The working water based Cu, Al2O3 and SWCNTs nanofluid flow is assigned to be Newtonian. The system of regulating equations are designated are
Employing Rosseland approximation for thermal radiation Sparrow and Cess [34], Rapits [35] and Brewster [36], qradn=-4σ1/3k* ∂T4/∂y, σ1- the Stefan-Boltzman constant, k* - the mean absorption coefficient. The Rosseland relation is recycled to define the thermal radiative heat transfer in the restraint of the optically thick fluid (nanofluid).
With boundary conditions
(Power index) are constants and V0 and Tw are (the suction (
V0 > 0 ) or injection ( V0 < 0 )) velocity and the fluid temperature at the
plate. The feasible flow velocity of the wedge is U(x,t)=v xm/δm+1,β1=2m/1+m Sattar [37] whereas δ is the time-dependent length scale, δ =δ (t)
and the Hartree pressure gradient parameter, β1=Ω/π,Ω - angle
of the wedge, the temperature of the fluid is simulated to differ
succeeding a power-law function while the free stream temperature
is linearly stratified. In equation (4) and n is a constant parameter
assigned as the thermal stratification parameter, 0 ≤ n <1. T0 =T∞ (0)
is a constant reference temperature. The suffixes w and ∞
denote surface and ambient conditions. Let u and v are the
velocity components along the x and y directions, T - the local
temperature of the nanofluid, g - the acceleration due to gravity,
K - the permeability of the porous medium, ρ fn- the effective
density of the nanofluid, rad q′′ - the applied absorption radiation
heat transfer, μ fn - the effective dynamic viscosity of the nanofluid,
α fn - the thermal diffusivity of the nanofluid, Aminossadati and
Ghasemi [38] which are defined aρs =(1 −ζ)ρf+ζρs, μfn=μf/(1 − ζ )2.5,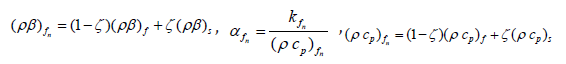 ,
,
Maxwell model [39] was refined to define the effective electrical or thermal conductivity of liquid-solid suspensions. Let kf and ks - the thermal conductivity of the base fluid and nanoparticle, ζ - the nanoparticle volume fraction, μf - the dynamic viscosity of the base fluid, βf and βs - the thermal expansion coefficients of the base fluid and nanoparticle, f ρ and ρs - the density of the base fluid and nanoparticle, kfn - the effective thermal conductivity of the nanofluid and (ρ cp)fn- the heat capacitance of the nanofluid.
Proposing the succeeding non-dimensional variables
Based on the above results, the equations (1) - (4) become
∂u/∂x+∂v/∂y=0 (7)
With boundary conditions
Pr= νf/αf- the Prandtl number,λ=δm+1/ K k2- the porous media
parameter, 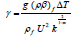 - the buoyancy or natural convection
parameter,
- the buoyancy or natural convection
parameter,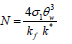 - the conductive radiation parameter, where θw=1/Tw-T∞≅0.1.Let
γ > 0 aids the flow and γ < 0 opposes the flow,
while γ = 0 i.e.( ) w T T∞ − , represents the case of forced convection
flow. Hence, combined convective flow exists when γ = O(1). Based on
Kafoussias and Nanousis [20]
- the conductive radiation parameter, where θw=1/Tw-T∞≅0.1.Let
γ > 0 aids the flow and γ < 0 opposes the flow,
while γ = 0 i.e.( ) w T T∞ − , represents the case of forced convection
flow. Hence, combined convective flow exists when γ = O(1). Based on
Kafoussias and Nanousis [20]
and θ=T-T∞/Tw-T∞,u=∂ψ/∂y and v=-∂ψ/∂x
The system of equations (7) - (9) become
With the boundary conditions
∂ψ/∂y=0,∂ψ/∂x=-V0,T=Tw at y=0,
where CT=T∞/Tw-T∞ - the temperature ratio, 0.1 T C = and heat radiation 0 ≤ N ≤1.0 , Murthy et al. [40].
The symmetry groups of Equs. (12) and (13) are estimated applying the classical Lie group approach as
It is noted that the form of infinitesimals as
g(x) - An arbitrary function.
Definitions of infinitesimal alternators are
The PDEs controlling the work under attention are converted by a exclusive mode of Lie symmetry group conversions viz. oneparameter infinitesimal Lie group of transformation into a system of ODEs. For the current situation, we considered that the generator 1 X with g(x) = 0 . The distinctive equations are
dx/x=dy/0=dψ/ψ=dθ/θ (18)
Based on the above equations, it is calculated as
η = y,ψ = x f(η ) and θ = xθ (η ) Where η =η (x,t) (19)
Established on these relations, the Equs. (12) and (13) become
S - The suction parameter if S > 0 and injection if S < 0 and
ξ =k x1-m/2 the dimensionless distance along the wedge (ξ > 0 ) [41].In this scheme of equations, it is predicted that the non similarity forms of the problem are exhibited in the terms involving partial derivatives with respect to ξ . Generation of the local nonsimilarity schemes with reference to the current work will now be reviewed. At the first level of truncation, the terms followed by ξ ∂/∂ξ are small. This is notably true when (ξ <<1). Therefore the terms with ξ ∂/∂ξ on the right-hand sides of Equations (20) and (21) are eliminated to obtain the succeeding scheme of equations:
With boundary conditions
Suppose that λυ= c/xm1, = , c is a constant so that c=δm/v ∂δ/∂t and integrating, it is predicted that δ = [c(m+1)ν t]1/ m+1 . In spite of c = 2 and m =1 in δ and we obtain δ = 2 ν t which observes that the parameter δ can be correlated with the well settled scaling parameter for the unsteady boundary layer problems [42].
For experimental principles, the functions f (η ) and θ (η ) grant us to define the skin friction coefficient and the Nusselt number as
Here, Rex=U x/v f = is the local Reynolds number.
Results and Discussion
Estimation are carried out by the fourth or fifth order Range Kutta Fehlberg method with shooting technique for different values of parameters. Equations (23) and (24) developed to the boundary conditions (25) have been resolved numerically employing computer software Maple 18. If γ >>1.0 conforms to pure free convection, γ =1.0 correlates to mixed convection and γ <<1.0 corresponds to pure forced convection. Impacts of nanoparticle shapes and solar thermal radiation energy on unsteady Hiemenz water based Cu, Al2O3 and SWCNTs nanofluid flow over a porous wedge sheet are investigated for different values of parameters. In order to justify our method, we have correlated the solutions of f (η ), f ′(η ) and f ′′(η ) for different values of η (Tables 1 & 2) with White [40] whereas f ′′(0) and θ ′(0) for distinct values of ξ (Table 3) with Vajravelu et al. [43] and observed them in desirable acknowledging.
Read More about Lupine Publishers Journal of Nanomedicine Please Click on Below Link: https://lupine-publishers-nano-science.blogspot.com/

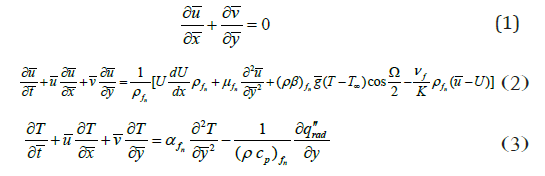
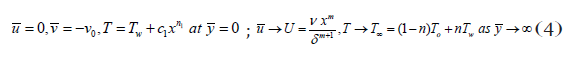
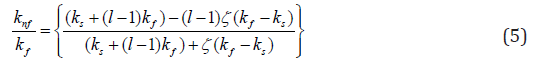
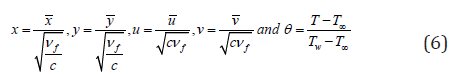
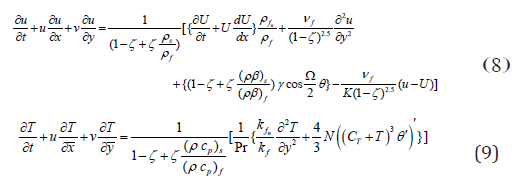
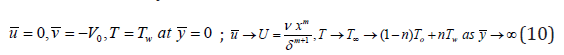
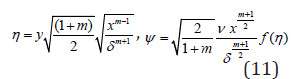
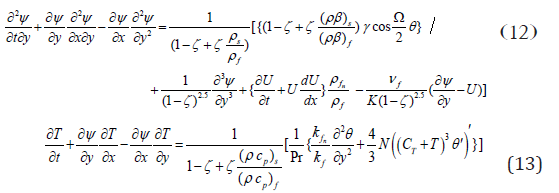
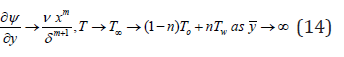
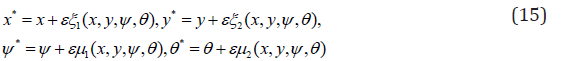
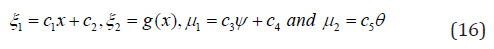
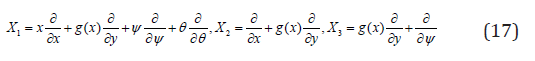
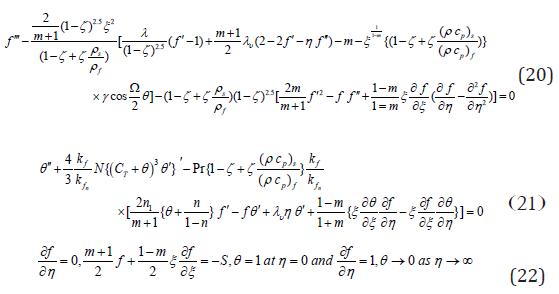
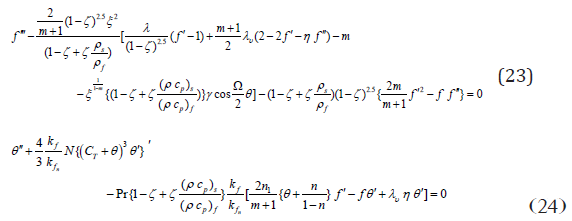
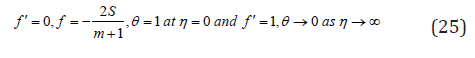
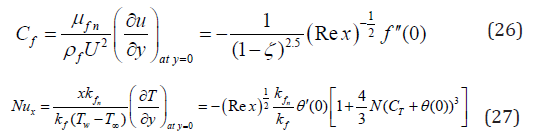
No comments:
Post a Comment
Note: only a member of this blog may post a comment.