Lupine Publishers| Current Trends in Computer Sciences & Applications (CTCSA)
Abstract
For a graph G, the second Zagreb eccentricity index E2(G) and eccentric connectivity index ∈c(G) are two eccentricity-based
invariants of graph G. In this paper we prove some results on the comparison between 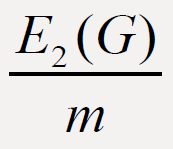 and
and 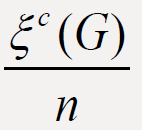 of connected graphs G of order
n and with m edges.
of connected graphs G of order
n and with m edges.
The authors demonstrated how a combination of both techniques and human interventions enhances control, decision-making and data analysis systems.
Keywords: Graph; Eccentricity (of vertex); Second Zagreb eccentricity index; Eccentric connectivity index
Introduction
Throughout this paper we only consider the note, undirected,
simple and connected graphs. The degree of v∈ V(G), denoted by
degG(v), is the number of vertices in G adjacent to v. For any two
vertices u; v in a graph G, the distance between them, denoted by
dG(u; v), is the length of a shortest path connecting them in G. As
usual, let Sn, Pn, Cn, Kn be the star graph, path graph, cycle graph
and complete graph, respectively, on n vertices. Other undefined
notations and terminology on the graph theory can be found in [1].
For any vertex of graph G, the eccentricity ∈G (v) (or ∈(v) for short)
is the maximum distance from v to other vertices of G, i.e., ∈G (v)=
maxu≠v dG(u,v). The eccentricity of a vertex is an important parameter
in pure graph theory. The radius of a graph G is denoted by r(G) and
defined by 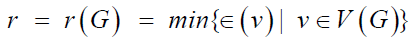 . Also, the diameter
of G, denoted by d(G), is the maximum distance between vertices
of a graph G and hence
. Also, the diameter
of G, denoted by d(G), is the maximum distance between vertices
of a graph G and hence 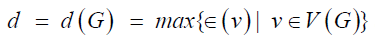 . A vertex
v with ∈G(v)= r(G) is called a central vertex in G. A graph G with
d(G) = r(G) is called a self-centered graph. A graph which contains
only two non-central vertices is called almost self-centered graph
[2] (ASC graph for short). Moreover, the eccentricity is also applied
in chemical graph theory. There are several eccentricity-based
topological indices, including the second Zagreb eccentricity index
E2(G) [3] and eccentric connectivity index ∈c (G) [4], of graphs G
where
. A vertex
v with ∈G(v)= r(G) is called a central vertex in G. A graph G with
d(G) = r(G) is called a self-centered graph. A graph which contains
only two non-central vertices is called almost self-centered graph
[2] (ASC graph for short). Moreover, the eccentricity is also applied
in chemical graph theory. There are several eccentricity-based
topological indices, including the second Zagreb eccentricity index
E2(G) [3] and eccentric connectivity index ∈c (G) [4], of graphs G
where 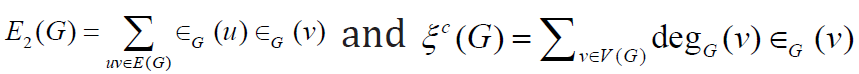
In particular, we have 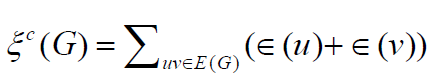 or any graph G.
In this paper we prove some comparison results between
or any graph G.
In this paper we prove some comparison results between 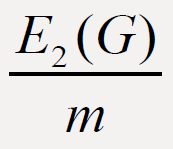 and
and
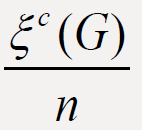 of connected graphs G of order n with m edges. Main results
In this we prove several results on the comparison between
of connected graphs G of order n with m edges. Main results
In this we prove several results on the comparison between 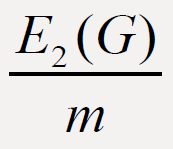 and
and 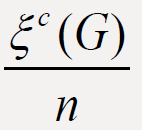 of graphs G. Firstly we present two useful lemmas.
of graphs G. Firstly we present two useful lemmas.
Lemma 2.1: [5] Let G be a connected graph of order n with maximum degree Δ . If Δ= n −1 then E2(G) =ξc(G) .Otherwise, E2(G) ≥ξc(G)with equality holds if and only if G is a 2-SC graph.
Lemma 2.1: [6] If u and v are two adjacent vertices of a connected graph G, then ∈(𝒰)−∈(𝒱) |≤1.
Denote by Gn(m; d) the set of connected graphs of order n with m edges and diameter d.
Theorem 2.3. Let G∈ζ(𝓂,𝒹) with n>5 and 𝒹≤2. Then 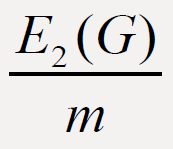 <
<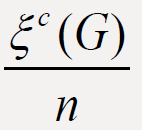 . Proof. If d = 1, G∈ζ(𝓂,𝒹) contains a single graph Kn
with
. Proof. If d = 1, G∈ζ(𝓂,𝒹) contains a single graph Kn
with 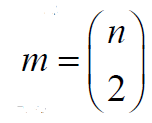 and
and 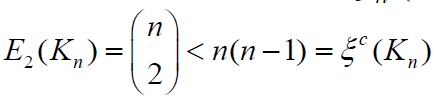 . Then our result follows. Next
it suffices to consider the case when d = 2. If G has maximum
degree Δ = n −1by Lemma 2.1, we have E2(G) <ξc(G) for any graph
G∈ζ(𝓂,𝒹) .Moreover, we have 𝓂≥𝓃−1 If 𝓂=n-1, then G≅Sn with
. Then our result follows. Next
it suffices to consider the case when d = 2. If G has maximum
degree Δ = n −1by Lemma 2.1, we have E2(G) <ξc(G) for any graph
G∈ζ(𝓂,𝒹) .Moreover, we have 𝓂≥𝓃−1 If 𝓂=n-1, then G≅Sn with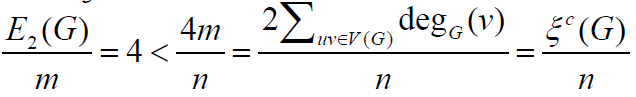 for any n ≥ 5. Moreover,
for any n ≥ 5. Moreover,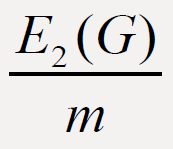 <
<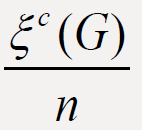 holds clearly
form ≥ n. If Δ ≤ n − 2 then G is a 2-SC graph. By Lemma 2.2, G is never
a tree. Therefore m ≥ n with equality holding if and only if G ≅ C4
or G ≅ C5 . Consider that n > 5, m > n holds immediately. It follows
that
holds clearly
form ≥ n. If Δ ≤ n − 2 then G is a 2-SC graph. By Lemma 2.2, G is never
a tree. Therefore m ≥ n with equality holding if and only if G ≅ C4
or G ≅ C5 . Consider that n > 5, m > n holds immediately. It follows
that 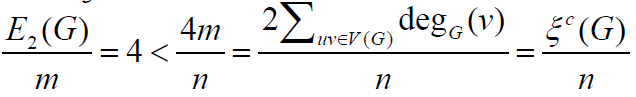 . This completes the proof of the
theorem.
. This completes the proof of the
theorem.
In the following we consider the graphs G∈ζ(𝓂,𝒹) with diameter d ≥ 3.
Theorem 2.4: Let G∈ζ(𝓂,𝒹). with d ≥ 3, n > 5 be a tree or a
unicyclic graph. Then 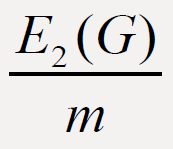 >
>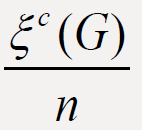 Proof. If d ≥ 3, then Δ(G) ≤ n − 2 .
From Lemma 2:1, we have E2(G) <ξc(G). Note that m ≥ n for any tree
or unicyclic graph G. Thus, it follows
Proof. If d ≥ 3, then Δ(G) ≤ n − 2 .
From Lemma 2:1, we have E2(G) <ξc(G). Note that m ≥ n for any tree
or unicyclic graph G. Thus, it follows 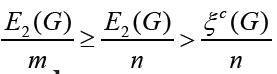 . finishing the
proof of the theorem. Next we consider the case
. finishing the
proof of the theorem. Next we consider the case
m > n. In the following theorem we give a sufficient condition
for the graph G of order n with 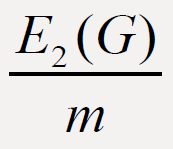 ≥
≥ 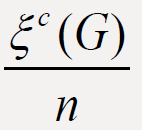 .
.
Theorem 2.5. Let G∈ζ(𝓂,𝒹) with d ≥ 3, m = n + t and 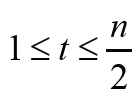 . If
r(G) ≥ 3, then
. If
r(G) ≥ 3, then 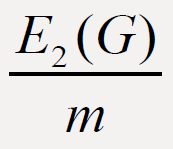 ≥
≥ 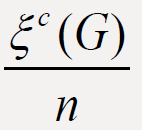 ,
,
Proof. Making a difference, we have 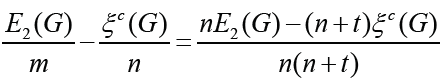
Set Δ1= nE2(G)−(n + t)ξc(G) . From Lemma 2.2, we have
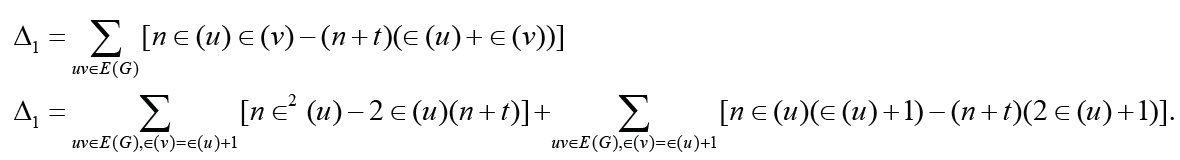
Since r(G) ≥3 and 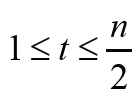 , we have
, we have
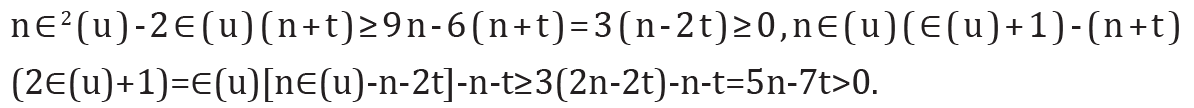
Therefore, Δ1 ≥ 0 with equality holding if and only if ∈(𝓊) = 3for each vertex 𝓊∈V(G) that is, G is a self-centered graph with radius 3. This completes the proof of the theorem.
F or, G∈ζ(𝓂,𝒹) with d ≥ 3, r = 2 and 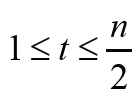 considering that
r(G)≤d(G)≤2r(G) we have d(G) = 3 or d(G) = 4. In this case, the value of Δ1 may be negative, zero or positive. Let
considering that
r(G)≤d(G)≤2r(G) we have d(G) = 3 or d(G) = 4. In this case, the value of Δ1 may be negative, zero or positive. Let
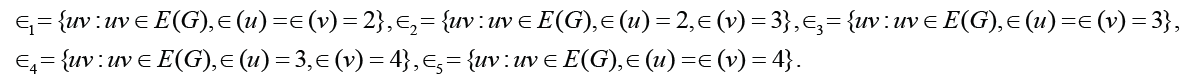
Denote by mi the cardinality of i∈{1, 2,3, 4,5}. Then
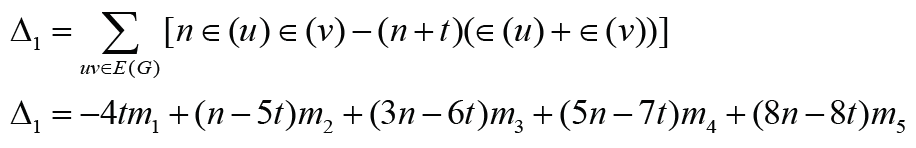
In the following result we present some comparison results for ASC graphs.
Theorem 2.6: Let G∈ζ(𝓂,𝒹) with d = 3, r = 2, m = n + t, t ≥ 1
where 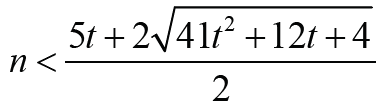 .
.
If G is an ASC graph, then 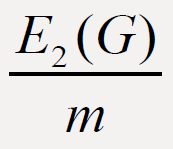 <
<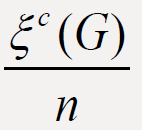 Proof. If G is an ASC
graph with d = 3, r = 2, from the structure of ASC graph, we have
𝓂3≤ 𝓃 − 2,𝓂3=0, that is, 1 𝓂 ≥ t + 2 . If 𝓃 ≤ 5t, clearly, we have Δ1 ≤ 0 .For n >
Proof. If G is an ASC
graph with d = 3, r = 2, from the structure of ASC graph, we have
𝓂3≤ 𝓃 − 2,𝓂3=0, that is, 1 𝓂 ≥ t + 2 . If 𝓃 ≤ 5t, clearly, we have Δ1 ≤ 0 .For n >
5t, we have
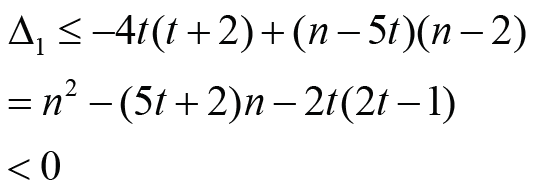
holds if and only if 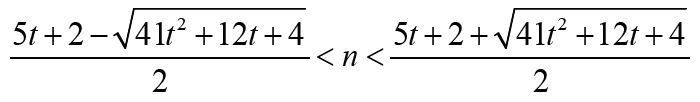 Note that
Note that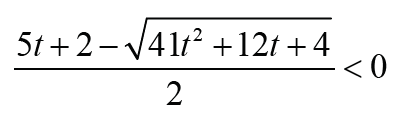 Thus Δ1 < 0 is equivalent that
Thus Δ1 < 0 is equivalent that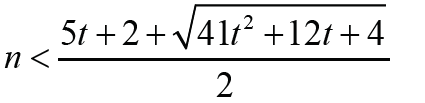 with t ≥1. Therefore the result holds immediately. It is much
interesting to search more generalized graphs G with different
comparison results between
with t ≥1. Therefore the result holds immediately. It is much
interesting to search more generalized graphs G with different
comparison results between 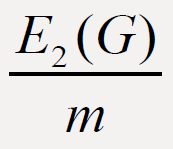 and
and 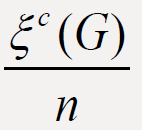 which can be a topic for
further research in the future.
which can be a topic for
further research in the future.
Read More About Lupine Publishers Current Trends in Computer Sciences & Applications (CTCSA) Please Click on Below Link: https://computer-sciences-lupine-publishers.blogspot.com/

No comments:
Post a Comment
Note: only a member of this blog may post a comment.