Lupine Publishers | Promising Role of Fractional Calculus in Biomedicine and Biophysics

 Lupine Publishers | Journal of Oncology

Introduction

The study of complex systems and investigation of their structural and dynamical properties have attracted considerable interests among scientists in general and physicists, biologists and medical researchers in particular. Complex systems can be found almost everywhere however the highest level of complexities is related to living and biological organisms and systems. Due to the lack of a reliable and effective tool to investigate such systems, we have not reached to the complete understanding and comprehensive pictures of the phenomena and processes which occur in these systems. Of course a comprehensive knowledge of biological and biomedical complex phenomena will be achieved when we employ simultaneously different field of science and engineering including: biology, chemistry, physics, mathematics, mechanical engineering and so on.

Fortunately in recent year's powerful tool of fractional calculus has been proposed for study of complex and nonlinear phenomena. It is in fact very useful tool for describing the behavior of nonlinear systems which are characterized by: special kind of non-locality, long-term memory and fractal properties. There exist many biological objects and systems with memory, nonlocal effects and nonlinear behaviors and such these non-localities and memory effects in biological objects and systems mean that the next state of the organism or system relies not only on its present state but also upon all of its previous states. As a result, the concept of fractional dynamics and in fact adopting fractional calculus can play an important role in the study of dynamical biological systems. Up to now few number of important issues such as: protein folding phenomena and mechanics of cancer cells (for more details see the references which have investigated physics of protein and physics of cancer in detail) have been investigated using the framework of fractional dynamics [1].

However many other important issues still remain as open issues, such as: modeling of interactions between light (laser) and biological tissue and modeling of intracellular (and intercellular) interactions in the framework of fractional dynamics. As a physicist or biologists and even medical researchers, we always are able to model natural phenomena for instance modeling of tumor growth using systems of differential equations and nowadays it is well know that the fractional-order ones are more comprehensive and also incorporate memory effect and the concept of non-locality in the model.

Mathematically the idea is in fact, to rewrite the ordinary governing differential equations in the fractional form by replacing the standard derivative with a fractional derivative of arbitrary order which is defined in the Caputo sense as follows:

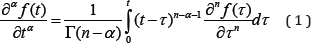
where Γ denotes the Gamma function and , . And its Laplace transform can be given by:

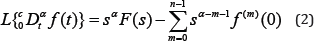
Where, F(s) is the Laplace transform of f (t). Solutions of fractional differential equations generally will be expressed using a generalized special function named as Mittag-Leffler function. This function can be considered as a generalized exponential function and has several different forms. For instance the one-parameter Mittag-Leffler function is defined by the series expansion as:

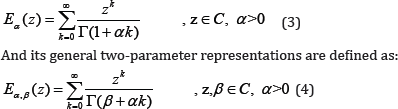
Where C is the set of complex numbers? It is worth mentioning that the exponential function is just a special case of α = l Mittag-Leffler function, for example for the special case of , the Mittag-Leffler function Eq. (3) reduces to the exponential function E₁(z) = e^z . This point is very important because of that the natural exponential function has been considered as a fundamental function of natural science and in particular biology up to now, so that many phenomena could be described using it and now scientist are able to think that with such this new framework (i.e. fractional differential equations and their solutions in terms of Mittag-Leffler functions) they can find many new results and information about biological and biomedical phenomena [2,3].

Finally, based on all above mentioned reasons, as a conclusion we should say that we believe that the powerful tool of fractional calculus and in fact the frame work of fractional dynamics can give.com new insights in understanding and modeling of nonlinear complex phenomena in various living cellular structures and their interactions and we invite all biologist and medical researchers to consider this new powerful approach for their future studies.

Read More About Lupine Publishers Journal of Oncology Please Click on Below Link:
https://lupine-publishers-cancer-journal.blogspot.com/