Lupine Publishers | Journal of Environmental & Soil Sciences
Abstract
Yield predictions allow for decision making regarding management of agricultural yield before and after harvest by government and decision-makers. Traditional approaches to collect yield statistics such as manual field surveys and physical computation of yield are costly and take a long time for information to be available. Remote sensing platforms such as hyperspectral data provide real-time, fast, and reliable statistics that can be used to derive yield information. Vegetation indices are ratios used to combine multiple band observations of the hyperspectral data into one index and applied to derive soybean grain yield. The objective of this study was to evaluate the potential of vegetation indices derived from hyperspectral data to predict soybean grain yield. Soybean hyperspectral data was acquired using a handheld spectroradiometer with a spectral range of 350 to 2500 nm in March and April of the summer season of 2017. The random forest regression algorithm was used to predict the soybean grain yield. NDVI, SR and EVI were calculated from the hyperspectral data for all probable bands situated in the 400 nm and 2399 regions. The results showed that relevant wavelengths in predicting soybean were combinations situated in the red-edge (680-750 nm), NIR and the MIR (1300 to 2399 nm) of the electromagnetic spectrum. Furthermore, regression results showed that SR better predicted the soybean grain yield (R2 = 0.843) compared to NDVI (R2 = 0.841) and EVI (R2 = 0.537). In overall, the results of this study suggest that narrow-band indices have the potential to predict soybean grain yield.
Keywords: Soybean Yield; Hyperspectral Data; Vegetation Indices
Abbreviations: NDVI: Normalised Difference Vegetation Index; SR: Simple Ratio; EVI: Enhanced Vegetation Index; RF: Random Forest; RMSE: Root Mean Square Error; FS: Free State; MP: Mpumalanga
Introduction
South Africa is the third dominant consumer of soybean in the world [1]. Mpumalanga, KwaZulu Natal and Free State provinces are the largest soybean producers in the country [2]. Over the last decade, soybean production and consumption in South Africa has increased [1,3]. Currently, soybean production does not meet South African local demands [3]. As a result, South Africa imports large quantities of soybean products [3]. Attaining higher yields entails increasing the area planted and/or use of more fertilisers [4]. Production in both approaches requires constant crop monitoring using reliable techniques that can provide real-time statistics. Constant monitoring of crops can enhance chances of attaining higher yield through early detection of problems that can potentially affect yield. Soybean yield information in the hands of farmers and policy makers is important for decisions such as planning for harvesting, yield management and market related decisions [5]. Thus, there is a need for an efficient real-time monitoring system to provide the status, growth and development of soybean information consistently that can enable yield predictions.
Various methods have been used to predict grain crop yields and these include the use of agricultural censuses, field surveys [6] and physical computation of yields by visiting numerous sample areas [7]. In South Africa, current yield predictions are based upon field surveys conducted telephonically, via emails, and or by post FAO [8]. However prediction methods based on traditional crop yields surveys are frequently subjective, susceptible to large inaccuracies and take a long time for information to be available for the benefit of food security and early planning before and during harvests [5]. In addition, yield predictions obtained influence the pricing of agricultural commodities and the decisions to be taken regarding imports and exports [8]. This therefore validates the need for crop monitoring initiatives that involve the use of reliable techniques such as remote sensing to ensure fair pricing of agricultural commodities and objective decision-making. Remote sensing methods are suitable; they include the acquisition of crop canopy measurements [9], and can deliver immediate, reliable, measurable evaluations of the ability of plants to capture radiation and photosynthesize [10]. These canopy spectral measurements are beneficial for estimating crop yield [9]. Research shows that remote sensing spectral bands have strong relationships with vegetation biomass [11].
Many researchers have used broadband multispectral data to predict yield of various crops such as maize [12], rice [5], soybean [10] and wheat [13,14]. Broadband multispectral data have advantages as it is applicable to regional areas and also because of numerous revisits of the same area as well as capturing data at large spatial scales in real-time [15]. In addition, multispectral data is available at low or no cost, which can be beneficial to countries with limited resources [15]. Despite these advantages, broadband data has drawbacks for vegetation observation such as exhibiting excessive spectral differences and shadows due to the above-ground coverage and landscape [11]. The latter can be a hindrance in producing precise biomass prediction models with the ability to distinguish between soil background and vegetation [11]. Precise biomass predictions are essential for effective monitoring and management of vegetation [11]. Furthermore, broadband data does not have specific narrow-bands that precisely focus on biochemical and biophysical factors of crops [16,17]. This suggests that multispectral broadband data exhibit difficulties in monitoring
crops with high biomass such as soybean. Although multispectral broadband data have these disadvantages, research has shown that these disadvantages can be overcome by the use of vegetation indices [18]. Vegetation indices eliminate differences caused by soil background, above-ground geometry, sun view angles as well as the influence of atmospheric circumstances when assessing biophysical characteristics of vegetation at aboveground scale [18]. Widely used vegetation indices for vegetation monitoring and modelling are calculated using the red and the near infrared (NIR) bands [19]. The red and NIR bands respond to the biochemical and biophysical properties of crops [16,19]. These spectral bands are sensitive to the rate of photosynthetic activity in green vegetation [20]. The Normalised Difference Vegetation Index (NDVI) [21] and Simple Ratio (SR) [22] are commonly utilised indices that are calculated using the NIR and the red bands [20] with applications for crop monitoring. Soybean has been monitored using NDVI modelled from broadband data sets such as AVHRR/NOAA [23,24] and ADAR 5500 4 band digital camera with a broadband width of 450 nm to 90 nm [25]. [26] used SR, NDVI, Soil Adjusted Vegetation Index (SAVI) and Transformed SAVI (TSAVI) to evaluate soybean biophysical properties such as yield, photosynthetically active radiation (PAR), leaf area index (LAI) and biomass [26]. Also, the SR index is known to be able to decrease the effect of soil background on the spectral reflectance and is also sensitive to changes occurring at prime developmental phases of vegetation [27]. The Enhanced Vegetation Index (EVI) is another widely used vegetation index in agricultural forecasting computed using the red and NIR bands with an addition of the blue band [28]. However, the EVI is insensitive to saturation when faced with high biomass vegetation [29]. Despite the usefulness of these spectral bands, broadband data is unresponsive to the variation in plant features [15].
Due to disadvantages encountered by broadband data, researchers promote the use of hyperspectral data that covers the whole range of the electromagnetic spectrum instead of just two or three bands [18]. Hyperspectral data provide advantages of handiness, flexibility, controllability and high temporal resolution, which are greatly beneficial in precision agriculture applications as opposed to satellite based platforms [30]. Also, hyperspectral data contains other important spectral bands such as the red edge bands that are useful in the study of vegetation [18]. The red edge band is highly responsive to variations in biomass of green vegetation [18]. Narrow bands are important for supplying more information with substantial enhancements compared to broad bands in enumerating biophysical properties of agricultural crops [17,31]. Also, hyperspectral data is important for modelling yield features of agricultural crops [17] such as chlorophyll content, photosynthetic activities and leaf structure [32]. Numerous researchers have used hyperspectral data for vegetation monitoring such as [17,18,31] with positive results. Mutanga and Skidmore [18] calculated NDVI from hyperspectral data and obtained that regular NDVI including strong chlorophyll absorption bands in the red region and NIR region inadequately predicted biomass (R2 =0.26). Whereas, the modified NDVI (MNDVI) that included bands in the range (700- 750 nm) and narrow-bands in the red-edge region (750-780 nm) showed a high predictive ability for biomass (R2 =0.77). Mariotto et al. [18] identified that important bands when modelling biophysical
properties of maize, wheat, cotton, rice and alfafa, (about 74% of them) are situated in the 1051-2331 nm regions. The remaining 30% of these bands are in the 970 nm region (10%), red-edge region (6%) and the visible region (10%) (Blue region (400-500nm), green region (501-600 nm) and NIR region (760-900 nm). Thenkabail et al. [31] concluded that stronger correlations with crop biophysical characteristics were situated in the red region (650-700 nm), shorter wavelengths of the green region (500-550 nm), the NIR region (900-940nm) and in the moisture sensitive area centred at 982 nm. Similarly, many researchers have used hyperspectral data to predict yield of agricultural crops such as lint [33], wheat [34], maize [35] and soybean [21]. However, for soybean [21] utilised spectral data acquired using a multispectral hand-held radiometer with a fewer number of bands. They obtained positive correlation between NDVI and soybean grain yield (R2 = 0.80). Research has shown that hyperspectral data has enabled estimation of yield of various crops and biomass of several vegetation types. However, soybean grain yield has not been predicted comprehensively using hyperspectral data in the spectral range of 400-2399 nm.
Hyperspectral data has however some limitations, such as those related to high dimensionality and redundancy [36] and the problem of multicollinearity [37]. As a result, identifying suitable bands for modelling is a challenging process. To overcome this problem researchers encourage the use of advanced statistical methods such as random forest (RF) regression algorithm [11]. Random forest is a regression algorithm that applies bootstrapping aggregation to create a group of trees based on the randomness of samples taken from the training data [38]. The random forest algorithm is known to be able to handle the high dimensionality of hyperspectral data and reduce data redundancy [37]. Also, random forest has been noted to perform better than other machine learning algorithms such as support vector machine and neural network because of its robustness against overfitting [11, 38-41]. The aim of this study was to evaluate the performance of narrow-band vegetation indices NDVI, SR and EVI derived from hyperspectral data in predicting soybean grain yield. The vegetation indices selected for the study are those frequently used for biomass or agricultural crop and ecological vegetation studies [18] and have been applied successfully in predicting other crops. The main objective of this study is to assess the relationships of narrow-band NDVI, SR and EVI to soybean grain yield. The second objective was to identify suitable narrow-band indices to predict soybean grain yield. The third objective was to compare the performance of NDVI, SR and EVI random forest models developed from narrow bands (400 nm to 2399 nm) in predicting soybean grain yield.
Materials and Methods
Study Sites
The research was conducted on two experimental farms located in the Free State Province of South Africa in Phuthaditjhaba (28°25’26”S and 28°56’12”E) and in the Mpumalanga province in Ermelo (26° 45’18” S and 30° 13’55” E) (Figure 1). The Free State and Mpumalanga provinces experience warm summers with high rainfall and cold winters. Both these areas receive approximately 625 mm of precipitation annually with most precipitation occurring in summer (October - March). The soil in Phuthaditjhaba can be characterised as “rich loam” type of soil [42] while the soil in Ermelo can be characterised as “low clay” [43] and sandy soil.
Figure 1: Map showing the location of the study sites in Free State (FS) and Mpumalanga (MP) provinces.

Experimental Setup
The experiment on both sites followed a split plot Randomized Complete Block Design (RCBD) method. In the two study sites, 72 experimental plots each with a size of 7 m length and 3 m width were used. The plots consisted of 7 rows with 60 cm row spacing. Three soybean cultivars from Pannar seeds (PANN 1500 R, PANN 1614 R and PANN 1664 R) were sown from the 13th to 15th December 2016 in the MP and from 19th to 21st of December 2016 in FS site. Fertilizer treatments of 0 kg, 30 kg and 60 kg of phosphorus (P) were applied to the plots to provide more nutrients and enhance the health of the soybean plants. The experiment consisted of three replicates and the soybean relied on rainwater for irrigation.
Field Spectral Measurements
The first set of field spectral measurements in Mpumalanga and Free State were taken in March 2017 and the second set of spectral measurements were taken in April 2017. During this period, the soybean had reached maximum canopy cover whereby the soil background could have little effect on the spectral measurements. Due to differences in planting date, the soybean in Mpumalanga was in the pod formation stage during the first visit while in the Free State site it was still flowering. Canopy spectral measurements were acquired during flowering, pod formation and seed filling stages randomly plot by plot across fertilizer treatments of 0 kg, 30 kg and 60 kg. An Analytical Spectral Device (ASD) Field Spec®3 optical sensor (Analytical Spectral Devices, Inc., Boulder, CO, USA) was used to take spectral measurements from 10:00 am to 14:00 pm local time (GMT+2). The spectroradiometer records wavelength ranging from 350 to 2500 nm, measuring radiation at 1.4 nm bandwidths for the spectral region of 350-1000 nm and registers 2 nm intervals for the spectral region of 1001-2500 nm [44]. The spectral measurements
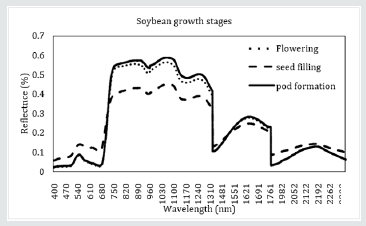
were taken under cloud free conditions. In each plot, 5 spectral measurements were taken with the optical cable connected to the spectroradiometer held at about 30 cm above the soybean canopy. Every 10 to 15 minutes a white reference spectralon calibration panel was used to balance any changes in the atmosphere and irradiance of the sun. The spectral measurements were added together to obtain the medial spectral measurements for each plot. Figure 2 shows average spectral reflectance of soybean at flowering, pod formation and seed filling stages. The spectral reflectance curve indicates the amount of radiation absorbed and reflected by the soybean at different regions of the spectrum. For soybean, the flowering and pod formation stages are critical stages in which the soybean utilises the absorbed radiation to photosynthesise and form grains [45]. A higher spectral signature is an indicator of a healthy crop in which higher yield can be expected whereas a low spectral signature indicates a lower yield [45].
Figure 2: Average spectral curves of soybean canopies at flowering, pod formation and seed filling stages.
Soybean Yield Data
To obtain soybean grain yield data, the soybean pods were harvested from the middle 3 rows of each plot at the end of the growing season of May and June 2017. The soybean pods were then crushed to obtain the soybean grains. The soybean grains obtained from each plot were weighed using the LBK1 weighing scale from ADAM Equipment [46]. The grains measurements of specific plots for each site were added to obtain the total yield of the soybean of each site.
Data analysiss
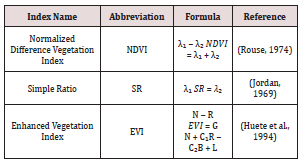
448 Bands allocated from 350 to 399 nm, 1350 to 1450 nm, 1800 to 1950 nm and 2400 to 2500 nm were omitted from the analysis due to atmospheric water absorption and the effect of noise in the reflectance spectra following techniques outlined in [11,36]. The remaining 1702 narrow-bands situated between 400 nm and 2399 nm were used to compute the narrow-band indices.The NDVI, SR and EVI indices were calculated using the standard indices equations [22, 28,47] (Table 1). These indices were calculated from all probable two-bands combinations including 1702 narrow bands situated between 400 and 2399 nm [11,18,19]. The narrow bands are presented as λ₁ (400-2399 nm) and λ₂ (400-2399 nm) combinations following approaches outlined in [18]. The calculated vegetation indices were correlated to the soybean yield using the Spearman’s correlation coefficient [2]. The correlations between vegetation indices and soybean grain yield were calculated to assess their relationship.
Assessing the Differences in Yields between Study Sites and Fertilizer Treatments
Exploratory data analysis was performed to understand the data before any statistical analysis was done. The statistical analysis was performed in STATISTICA 13 software testing for normalcy of the data using Lilliefors test [48]. Furthermore, an analysis of variance was performed to determine if there were differences in soybean grain yield means between the two study sites and between the three fertilizer treatments.
Statistical Analysis Using the Random forest (RF) Regression
The random forest regression technique was used to predict the soybean grain yield. RF is a machine learning algorithm developed by Breiman [49] that applies a bootstrap aggregation method in which an ensemble of trees (ntree) are developed on the basis of the randomness of samples extracted from the training data. For regression, the random forest permits trees to grow to the highest magnitude without trimming, depending on the bootstrap sample from the training data [49]. At every tree, the RF grows a randomized subgroup of predictors (mtry) to identify the optimum split at every node of the tree [41]. At the end, the RF averages the outcome of the overall sum of trees in order to obtain the overall estimation [50]. From the bootstrap samples of the training data (2/3), each tree grows randomly and selected independently. The residual original data (1/3) of the excluded samples (called outof-bag (OOB)) are then used to validate the model and predict variables of importance [51,52].
RF requires two parameters to be tuned that are (i) (ntree) the number of trees to grow and (ii) (mtry) the number of variables that are split at each node [41]. The ntree and the mtry parameters (vegetation indices) were then optimized for the random forest model using the top 20 NDVI, SR and EVI data sets to determine the best index that can be used to predict soybean grain yield. The mtry was calculated for all probable band combinations while the ntree was evaluated at 500, 1000, 1500, 2000, 2500, 3000, 3500, 4000, 4500, and 5000 trees. The random forest model was developed from 70% (2/3) of the training data to build a model that can predict soybean grain yield (g/m2 ) and 30% (1/3) of the test data was used to validate the model (OOB). Important indices at predicting soybean grain yield were selected by the RF using the permutation variable importance measures (mean decrease in accuracy). The RF algorithm was implemented using the R statistical software using the random Forest built in package to predict the soybean grain yield (Liaw and Wiener, 2002).
Variable Importance Selection
Random forest calculates variable importance using the Gini index and the permutation variable importance measures [53]. The permutation variable importance measure is defined as the variation between the OOB error from the data set acquired by random selection of the predictor variables and the OOB error from the original data set [53]. While the Gini index variable importance is a measure used in a classification when growing trees in the random forest [54]. The permutation variable importance measure is the most preferred measure of importance as it assesses importance of variables using the mean decrease in accuracy in the OOB predictions as forests are being assembled [53]. Permutation variable importance predicts the importance of a variable by determining how much prediction error rises when a variable is selected while others remain the same [55,56]. For this study, the permutation variable importance was used to determine the combination of indices that were powerful than the others in predicting soybean grain yield. From the ranking of the mean decrease in accuracy, the top 3 important combinations of indices were selected.
Accuracy Assessment
When using the random forest, research has shown that there is no need for a different test data for validation because the random forest uses an OOB error prediction built internally [37,38,50,57,58]. This is particularly remarkable in situations where data acquisition is highly dependent on oscillating weather conditions. The random forest computes the OOB error as a result of variance between the estimation made using the training data set and the OOB data set [41,59]. OOB error produces an unbiased evaluation of the prediction accuracy of the model [40]. The coefficient of determination (R2 ) and root mean square error (RMSE) were reported on the assessment of the accuracy of the random forest models. RMSE was calculated using the formula below:
where Ŷ and Y are measured and predicted soybean grain yield respectively.
Results
Assessing the Differences in Soybean Yields between Study Sites and Fertilizer Treatments
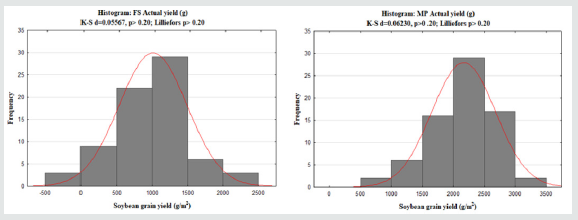
Exploratory statistics showed that soybean grain yield data does not significantly deviate away from a normal distribution for both sites (Figure 3) and thus meets the assumptions of ANOVA. Analysis of variance results showed that there were significant differences between the soybean grain yield in Free State and
Mpumalanga provinces (p≤0.05). However, the results showed no significant differences in soybean grain yield between fertilizer treatments on the study sites (p≥0.05). The total soybean grain yield obtained in FS was 72816 g/m2 with an average of 1011.3 g/m2 per field while the total soybean grain yield in MP was 156060 g/m2 with an average of 2167.5 g/m2 per field. In total, the soybean grain yield of both sites was 228876 g/m2 with an average of 1589.4 g/m2.
Narrow-Band NDVI and SR Relationship to Soybean Grain Yield
Table 2: Top 20 narrow band NDVI indices (λ=30 nm) that produced the highest correlation coefficients with soybean grain yield.
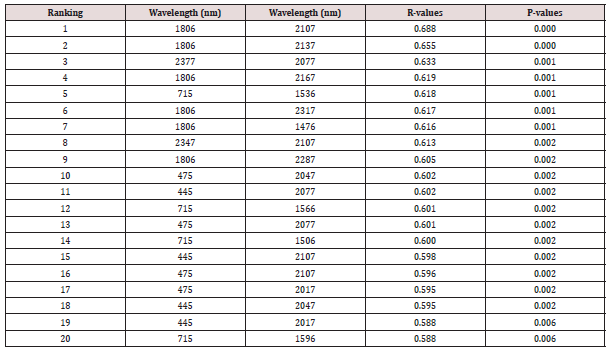
Narrow-band NDVI and SR were computed for all probable two-band combinations in the spectral range 400 nm to 2399 nm. Spearman’s correlation coefficients were applied to assess the relationships of the narrow-band NDVI and SR to soybean yields. The NDVI and SR obtained identical results of the correlations to the soybean grain yield (Tables 2 & 3). The correlation coefficients (R) results obtained between NDVI/SR and soybean grain yield ranged from 0.00 to 0.68 shown in Tables 2 & 3.
Table 3: Top 20 narrow band SR indices (λ=30 nm) that produced the highest correlation coefficients with soybean grain yield.
Figures 4 & 5 depict a graphical presentation of the R-values for the relationship between soybean grain yield and NDVI and SR. These results show a moderate to strong relationship between NDVI/SR and the soybean grain yield (R-values from 0.588 to 0.688). In addition, the p-vales obtained for these results indicate that the relationships between soybean grain yield and the derived vegetation indices are significant as they are less that 0.05. Correlation coefficients of NDVI and SR were arranged in the order of the highest to the lowest and the top 20 R-values. The top 20 best NDVI/SR indices are situated in the blue (445 nm - 475 nm), rededge (715 nm) and in the MIR regions (1506 nm – 2377 nm) of the electromagnetic spectrum (Figures 4 & 5).
Figure 4: Heat map showing the correlation coefficients (R) between soybean grain yield and narrow band NDV acquired from all probable band combinations from the spectral range of 400 nm to 2399 nm.
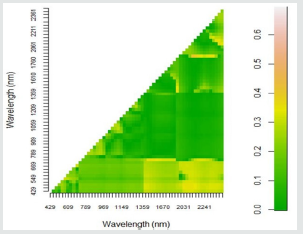
Figure 5: Heat map showing the correlation coefficients (R) between soybean grain yield and narrow band SR acquired from all probable band combinations from the spectral range of 400 nm to 2399 nm.
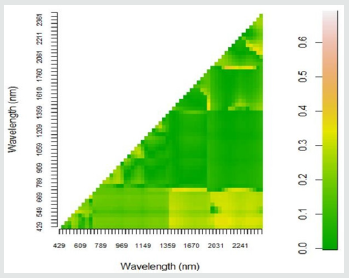
Narrow-Band EVI Relationship to Soybean Grain Yield
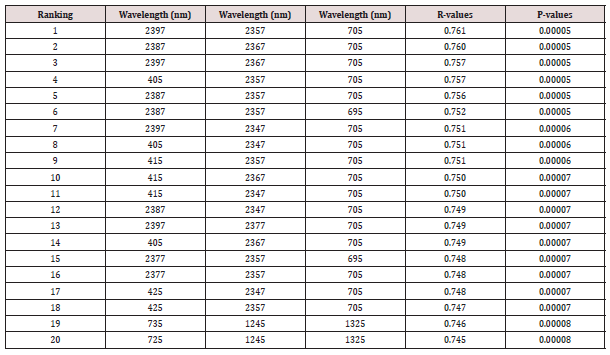
Narrow-band EVI was computed from all probable band combinations in the spectral range of 400 to 2399 nm of the electromagnetic spectrum. Spearman’s correlation coefficients were calculated to assess the relationship between the EVI indices and the soybean grain yields. The correlation coefficient results of EVI indices ranged from 0.00 and 0.761. The relationship between soybean grain yield and the derived narrow- band EVI are significant as shown by the p-values less than 0.05 in Table 4. Correlation coefficients of the narrow-band EVI were ranked from the highest to the lowest and the top 20 best indices were selected and shown in Table 4. The best 20 EVIs are situated in the blue region (405 nm – 425 nm), red region (695 nm), red-edge ((705 nm- 735 nm) NIR (1245 nm) and the MIR (2357 nm– 2397 nm) regions of the electromagnetic spectrum.
Table 4: Top 20 narrow-band EVI indices (λ= 10 nm) that produced the highest correlation coefficients with soybean grain yield.
Optimization of the Random Forest Regression Models
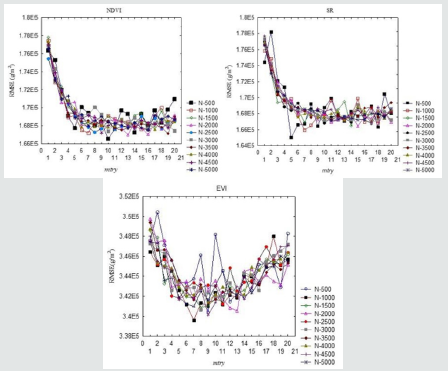
For the three indices (NDVI, SR and EVI), the ntree and mtry values were optimized using the training dataset to identify values that best predicted soybean grain yield. For each index, ntree values from 500 to 5000 were tested and mtry was tested from 1 to 20 (Figure 6). The mtry and ntree values that produced the best RMSE were selected. According to the results (Figure 2), the best mtry for the NDVI and SR models were 10 and 5 and their ntree was 500 respectively. For EVI, the best mtry was 7 and the ntree was 1000.
Variable Importance of Narrow-Band Indices in Predicting Soybean Grain Yield Using the RF
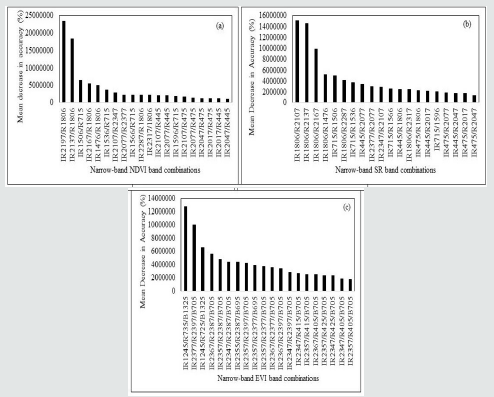
From the best 20 selected indices that were highly correlated with the soybean grain yield, it was essential to categorize narrowband indices of NDVI, SR and EVI that would highly perform when predicting soybean grain yield (g/m2 ). The RF calculated variable importance using the mean decrease in accuracy to measure the importance of NDVI, SR and EVI at predicting soybean grain yield (g/m2 ). The RF algorithm was capable of ranking the NDVI (Figure 7a), SR (Figure 7b) and EVI (Figure 7c) indices according to their importance in predicting soybean grain yield.
Using the mean decrease in accuracy arrangement, top 3 wavelength combinations that had significant importance in predicting the soybean grain yield were selected. For NDVI, top 3 band combinations included:
(i) 2197 nm and 1806 nm,
(ii) 2137 nm and 1806 nm and
(iii) 1506 nm and 715 nm. similarly,
SR top 3 important wavelength combinations include
(i) 1806 nm and 2107 nm,
(ii) 1806 nm and 2137 nm and
(iii) 1806 nm and 2167 nm. In addition,
EVI top three significant wavelengths included
(i) 1245 nm, 735 nm and 1325 nm,
(ii) 2377 nm, 2397 nm and 705 nm and
(iii) 1245 nm, 725 nm and 1325 nm.
Figure 7: Mean Decrease in Accuracy (%) of NDVI (a), SR (b) and EVI (c) concluded by the random forest algorithm. Important variables ranked are those with the highest mean decrease accuracy.
Accuracy Assessment
Figure 8: Random Forest models (NDVI (a), SR (b) and EVI (c)) showing sensitivity of ntree to the OOB error.
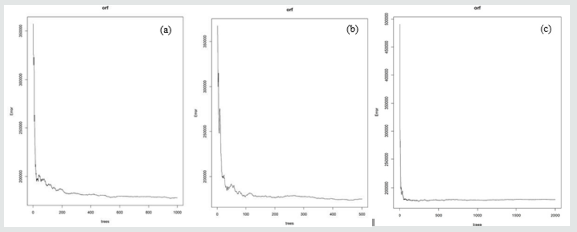
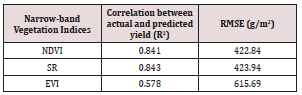
Figure 8 shows the best ntree results of the RF models for NDVI (a), SR (b) and EVI (c). This indicates that for NDVI and SR, the models obtained accuracy at 500 trees and at 1000 trees for EVI. The coefficient of determination (R2 ) and Root Mean Square Error (RMSE) were statistical measures that were used to evaluate the predictive performance and accuracy of the random forest regression models (NDVI, SR and EVI). Table 5, shows the performance results of the random forest prediction models. The results show that SR obtained the highest R2 of 0.843 with a RMSE of SR= 423.94 and RMSE of NDVI=422.84 (26.11% of the average soybean grain yield) compared to NDVI that obtained R2 =0.841 with an RMSE of 423.94 (26.04% of the average soybean grain yield) and EVI (R2 = 0.578) (37.04% of the average soybean grain yield) and RMSE of 615.94. These results suggest that SR can better predict soybean, however NDVI obtained better accuracy in the prediction in comparison to SR and EVI.
Table 5: Predictive performance of the NDVI, SR and EVI random forest prediction models using top 20 best indices.
Discussion
The aim of the study was to evaluate the potential of narrowband indices (NDVI, SR and EVI) in predicting soybean grain yield (g/m2 ). Broadly, the results of this study demonstrated that narrowband situated in the blue, red, red edge and MIR regions have a potential to predict soybean grain yield. The objectives were to assess the relationships of the narrow-band indices to the soybean grain yield, identify suitable narrow- band indices to predict soybean and to compare the accuracy of the prediction models. The study further showed that important bands in predicting soybean grain yield are not only bands in the NIR and red regions but also bands situated in the MIR region.
Assessment of the Relationships of Narrow-Band Indices to Soybean Grain Yield
The R-values obtained for NDVI (0.00-0.688), SR (0.00-0.688) and EVI (0.00-0.761) showed that different combinations of bands respond differently to variations in soybean grain yield. As shown in Tables 2-4, strong correlations to the soybean grain yield did not only consist of combinations of bands in the red and NIR regions. Strongly correlated indices of NDVI, SR and EVI to soybean consisted of combinations of bands in the blue region (405 nm - 475 nm), red region (695 nm), red edge (705-735 nm), NIR (1245 nm) and the MIR regions (1325 nm -2397 nm). These results correspond with those reported by Mutanga and Skidmore [18], which suggested that information on vegetation biomass is not only limited in the red and NIR bands. As a result, NDVI, SR and EVI highest correlations mainly consisted of combinations of bands in the MIR (1300-2399 nm) and combinations of the blue (400- 500 nm) bands and red-edge (700-729 nm) bands. The MIR region is known to be sensitive to water content of leaves and has low reflectance [32]. However, for this study, most MIR bands showed strong sensitivity to biochemical factors found in soybean such as nitrogen, protein as well as oil [32]. Similarly, wavelengths in the blue region are highly sensitive to chlorophyll a and b since plants absorb the violet-blue light for photosynthesis [32]. Based on these results it is understandable that combinations of these bands would obtain the highest correlation to the soybean grain yield. These results also concur with those reported by Darvishzadeh et al. [60,17]. Darvishzadeh et al. [60], showed that bands in the MIR had the strongest relationship to leaf area index (LAI) compared to the red and NIR bands. Mariotto et al. [17], reported that about 74% of bands sensitive to biophysical properties were situated in the MIR (1051 to 2331 nm). Additionally, the red-edge band is characterised by high reflectance and is linked to differences in the chlorophyll content that is associated with biomass of vegetation [18,32]. It is reasonable that combinations of wavelengths including the red- edge would obtain a strong relationship to soybean grain yield. Generally, these results provided more understanding of the relationship of the soybean grain yield and its significant wavelength regions. Furthermore, the results showed that important information on soybean yield is mostly contained in the MIR (1300 to 2399 nm) and indicate that narrow-bands have the potential to predict soybean grain yield.
Variable Importance and Assessment of the Predictive Performance of the NDVI, SR and EVI Random Forest Models
In the top 20 selected indices that had a strong relationship to soybean grain yield, it was necessary to identify which of those were significant in the prediction of soybean grain yield. The random forest used the mean decrease in accuracy measures to identify combinations of bands that are most significant in the prediction of soybean grain yield. The results of the optimization of the random forest showed that 10, 5, and 7 indices (NDVI, SR and EVI) out of 20 indices (predictors) at 500 and 1000 ntrees were significant at predicting soybean grain yield. These results further demonstrated that accuracy of the prediction was obtained with a smaller number of trees (ntree=500) compared to a larger number of trees (ntree = 1000). These results were validated by the differences in RMSE of 423.94 at 500 ntree compared to the RMSE = 615.69 at 1000 ntree. The obtained results concur with those of Abdel-Rahman et al. [41] who suggested that fewer number of trees (ntree) results in lower RMSE, which indicates better accuracy. The R2 results of the NDVI, SR and EVI random forest models showed that SR obtained the highest R2 in predicting soybean grain yield. These results indicate that, compared to the NDVI and EVI, SR is a better index at predicting soybean grain yield. These findings are similar to those obtained by Mutanga and Skidmore [18] who in their study concluded that SR (R2 =0.80) was a better index at predicting biomass in dense canopies than NDVI and Transformed Vegetation Index (TVI). Higher performance of SR could be because of its high sensitivity to high biomass as compared to NDVI which saturates when faced with high biomass [61,62]. Although the SR obtained the highest R2 , the NDVI obtained the lowest RMSE of 422.84 compared to SR (RMSE=423.94) and EVI (RMSE=615.69). These findings indicate that NDVI has better accuracy at predicting soybean yield since a lower RMSE indicates better accuracy. In conclusion, these results suggest that both the SR and NDVI can accurately predict soybean grain yield.
Conclusion
This study shows the success of narrow-band indices in predicting soybean grain yield. The results have shown that important narrow-bands in predicting soybean grain yield are not only combinations of bands situated in the red (695 nm) and the NIR (1245 nm) regions but are also combinations of bands found in the blue region (405 nm - 475 nm), red edge (705 nm -735 nm) and the MIR regions (1325 nm -2397) nm. Furthermore, the SR index (R2 = 0.843) proved to be a better index in predicting soybean grain yield compared to the NDVI (R2 = 0.841) and EVI (R2 = 0.578).
Acknowledgement
We acknowledge the Agricultural Research Council (ARC), the National Research Foundation (NRF) and the University of the Free State for the financial support for this study. We thank the Soil Science division in ARC that allowed us to collect soybean reflectance data from their experimental farms. Thank you to Dr Solomon Newete and Eric Economon for their assistance in acquiring spectral reflectance data.
Read More About Lupine Publishers Journal of Environmental & Soil Sciences Please Click on Below Link:
https://lupine-environmental-soil-sciences.blogspot.com/

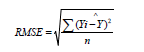
No comments:
Post a Comment
Note: only a member of this blog may post a comment.