Lupine Publishers| Some Simple Mathematical Models in Epilepsy

 Lupine Publishers| Journal of Biostatistics & Biometrics

Abstract

Epilepsy is a chronic disorder of the brain that affects people of all ages. Here epileptic seizures equations are related to the telegraph equation.

Introduction

Some Basic Facts about Epilepsy

Epilepsy is a chronic disorder of the brain that affects people of all ages. Approximately 50 million people worldwide have epilepsy, making it one of the most common neurological diseases globally. People with epilepsy respond to treatment approximately 70% of the time. About three fourths of people with epilepsy living in lowand middle- income countries do not get the treatment they need. Therefore, using different approaches to study epilepsy is useful [1].

2.2. Telegraph Equation in Epilepsy

Telegraph equation [2,3] is a generalization of diffusion equation where the standard diffusion equation depends on the continuity equation and Fick’s law

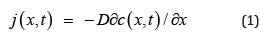
Where,

j is the diffusing object (e. g. technology, concept, etc...),

c is the distribution function of this object and

D is the diffusion constant.

The resulting standard diffusion equation is

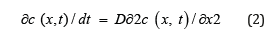
where is the second order differentiation w. r. t. position x.

A basic weakness of this equation is that the flux j reacts simultaneously to the gradient of c and consequently an unbounded propagation speed is assumed. To solve this problem Fick’s law is replaced by

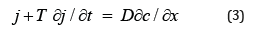
where T is a time constant which measures the memory or delay effect. Thus, one gets the telegraph equation:

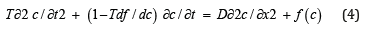
Applying this equation to the case

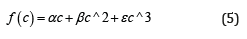
and making the identifications

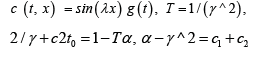
one regains equations 1-4 in [4] where t0 is small and we made the expansion

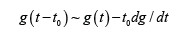
These equations are used to explain dynamical properties of epileptic seizures.

Read More about Lupine Publishers Journal of Biostatistics & Biometrics Please Click on Below Link:
https://lupine-publishers-biostatistics.blogspot.com/