Lupine Publishers| On some Derivatives of Vector-Matrix Products Useful for Statistics

 Lupine Publishers| Journal of Biostatistics & Biometrics

Mini Review

In this brief description, we will use the numerator layout [1], and will tacitly assume that all products are conformable.

The derivative of the linear form 𝒰^t𝒱 with respect to the vector 𝒱is given as

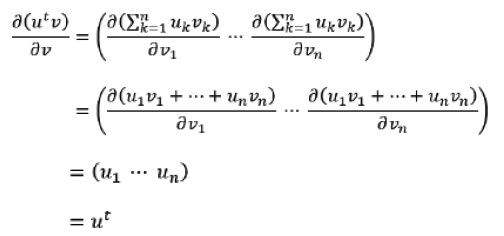
and since 𝒰^t𝒱 is a scalar, we are facing a particular case of the derivative of a scalar λ with respect to a vector, e.g., ∂_𝒱λ=(∂_𝒱1λ ..... ∂_𝒱nλ) and it must also be ∂_𝒱(𝒰^t𝒱)=∂_𝒱(𝒱^t𝒰) . Moreover, it is easy to demonstrate that using the denominator layout, the derivative would have been ∂_𝒱(𝒰^t𝒱)=𝒰

If both 𝒰 and 𝒱 vectors are function of a third vector 𝒵, we get

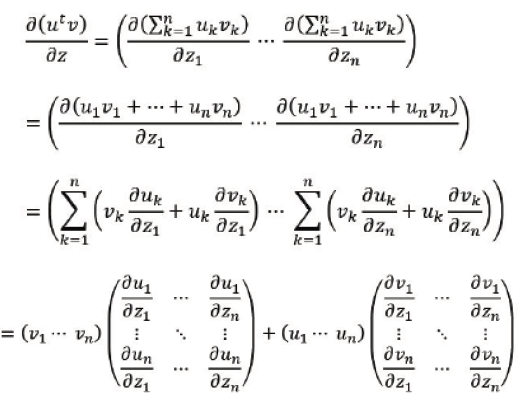
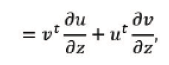
which, in the case 𝒰=𝒱=𝒲 reduces to

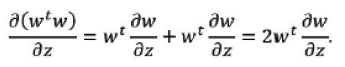
Dealing with a linear transform 𝒰=a𝒱, if A is 𝓂×𝓂 we have

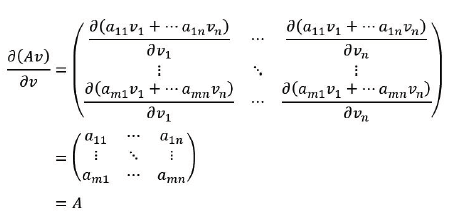
and if 𝒱 is a function of a vector 𝒲_𝒱 we get

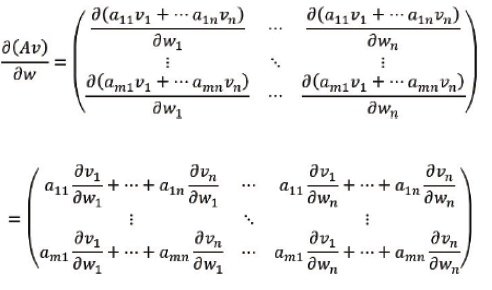
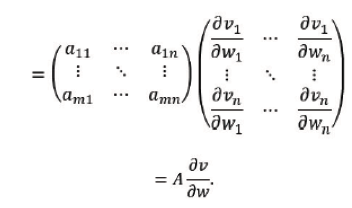
From definition of bilinear form, we obtain, for 𝒰^tA𝒱 the derivative

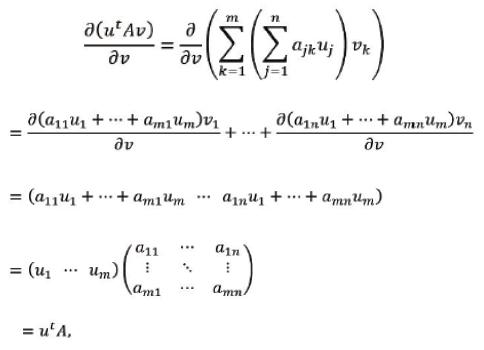
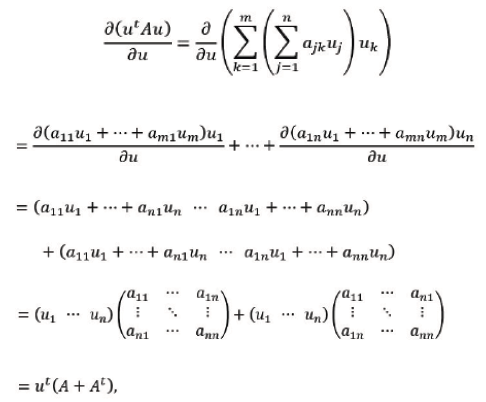
while, for a quadratic form 𝒰^tA𝒱(where A is 𝓃 × 𝓃), we get

Read More About Lupine Publishers Journal of Biostatistics & Biometrics Please Click on Below Link: https://lupine-publishers-biostatistics.blogspot.com/