Lupine Publishers | The Transfiguration with Self-Phase Modulation Effect of Entanglement in A Plasmatic Moving Frame

 Lupine Publishers | Journal of Otolaryngology

Abstract

In quantum optics, the Heisenberg picture, in which the optical fields can be treated as conjugate positions and momenta of quantized harmonic oscillators, as it is easy to substitute optical fields in classical electromagnetic problems with noncommutative operators and obtain the Heisenberg equations of motion. Once the operator equations are solved, it is possible obtain various quantum properties of the optical fields via noncommutative algebra. The Heisenberg picture is often not without shortcomings. Its difficulties have led to a growing appreciation of the Schrödinger picture, where the photons are treated as an ensemble of bosons and the evolution of the many-photon probability can be used. This is more intuitive approach that has led to great success in the quantum theory of solitons. Instead of solving the formidable nonlinear operator equations, we can obtain analytic solutions from the linear boson equations in plasmatic the Schrödinger picture which lead to the theory of Plasmatic Moving Frames.

Keywords: The Heisenberg Picture; The Optical Fields; The Plasma in Physics; Plasma in Medicine; The Many Photon Probability; Solitons, The Schrödinger Picture; Nonlinear Operator Equations; Plasmatic Moving Frame

Introduction

Plasma

(Figure 1) Plasma (from Ancient Greek πλάσμα, meaning ‘moldable substance [1]) is one of the four fundamental states of matter, and was first described by chemist Irving Langmuir [2] in the 1920s [3]. Plasma can be artificially generated by heating or subjecting a neutral gas to a strong electromagnetic field to the point where an ionized gaseous substance becomes increasingly electrically conductive, and long-range electromagnetic fields dominate the behaviour of the matter [4]. Plasma and ionized gases have properties and display behaviors unlike those of the other states, and the transition between them is mostly a matter of nomenclature [2] and subject to interpretation [5]. Based on the surrounding environmental temperature and density, partially ionized or fully ionized forms of plasma may be produced. Neon signs and lightning are examples of partially ionized plasma [6]. The Earth’s ionosphere is a plasma and the magnetosphere contains plasma in the Earth’s surrounding space environment. The interior of the Sun is an example of fully ionized plasma, [7] along with the solar corona [8] and stars [9]. Positive charges in ions are achieved by stripping away electrons orbiting the atomic nuclei, where the total number of electrons removed is related to either increasing temperature or the local density of other ionized matter. This also can be accompanied by the dissociation of molecular bonds, [10] though this process is distinctly different from chemical processes of ion interactions in liquids or the behaviour of shared ions in metals. The response of plasma to electromagnetic fields is used in many modern technological devices, such as plasma televisions or plasma etching [11]. Plasma may be the most abundant form of ordinary matter in the universe, [12] although this hypothesis is currently tentative based on the existence and unknown properties of dark matter. Plasma is mostly associated with stars, extending to the rarefied intracluster medium and possibly the intergalactic regions [13].

Definition

Plasma is a state of matter in which an ionized gaseous substance becomes highly electrically conductive to the point that long-range electric and magnetic fields dominate the behaviour of the matter. The plasma state can be contrasted with the other states: solid, liquid, and gas. Plasma is an electrically neutral medium of unbound positive and negative particles (i.e. the overall charge of a plasma is roughly zero). Although these particles are unbound, they are not “free” in the sense of not experiencing forces. Moving charged particles generate an electric current within a magnetic field, and any movement of a charged plasma particle affects and is affected by the fields created by the other charges. In turn this governs collective behaviour with many degrees of variation [10].

Figure 1: Top: Lightning and neon lights are commonplace generators of plasma. Bottom left: A plasma globe, illustrating some of the more complex plasma.

Mathematical Descriptions

(Figure 2) The complex self-constricting magnetic field lines and current paths in a field aligned Birkeland current that can develop in a plasma. To completely describe the state of a plasma, all of the particle locations and velocities that describe the electromagnetic field in the plasma region would need to be written down. However, it is generally not practical or necessary to keep track of all the particles in a plasma. Therefore, plasma physicists commonly use less detailed descriptions, of which there are two main types:

Figure 2.

a) Fluid Model

Fluid models describe plasmas in terms of smoothed quantities, like density and averaged velocity around each position (see Plasma parameters). One simple fluid model, magnetohydrodynamics, treats the plasma as a single fluid governed by a combination of Maxwell’s equations and the Navier–Stokes equations. A more general description is the two-fluid plasma picture, where the ions and electrons are described separately. Fluid models are often accurate when collisional is sufficiently high to keep the plasma velocity distribution close to a Maxwell–Boltzmann distribution. Because fluid models usually describe the plasma in terms of a single flow at a certain temperature at each spatial location, they can neither capture velocity space structures like beams or double layers, nor resolve wave-particle effects.

b) Kinetic Model

Kinetic models describe the particle velocity distribution function at each point in the plasma and therefore do not need to assume a Maxwell–Boltzmann distribution. A kinetic description is often necessary for collision less plasmas. There are two common approaches to kinetic description of a plasma. One is based on representing the smoothed distribution function on a grid in velocity and position. The other, known as the particle-in-cell (PIC) technique, includes kinetic information by following the trajectories of a large number of individual particles. Kinetic models are generally more computationally intensive than fluid models. The Vlasov equation may be used to describe the dynamics of a system of charged particles interacting with an electromagnetic field. In magnetized plasmas, a gyrokinetic approach can substantially reduce the computational expense of a fully kinetic simulation.

c) The spatiotemporal entanglement evolution in free space

The many-boson interpretation may be applied to study of entangled photons as well, where the two-photon probability is used to obey the Wolf equations by Saleh, Teich, and Sergijenko (STS). Instead of treating the entanglement properties of the photons, and the optical propagation as two separate problems, with the STS equations, we can use now a single quantity – namely, the two-photon amplitude – to keep track of the spatiotemporal entanglement evolution in free space. This is analogous to the Wolf equations, which reformulate the laws of optics in terms of coherence propagation. We utilize the STS treatment of the two photons in study of various temporal effects. The Schrödinger picture would offer a more accessible interpretation of temporal entanglement propagation for studies of two-photon systems. For example, a four-wave mixing in a coherently prepared atomic gas, thus extending the STS model for use in many more topics in quantum optics in order to demonstrate the use and intuitiveness of the Schrödinger picture. Based on this formalism, we propose the concept of quantum plasmatic temporal imaging, which uses dispersive elements and temporal phase modulators to manipulate the temporal entanglement properties of two photons. It is possible to convert positive-time correlation to negative-time correlation, or vice versa, using a plasmatic temporal imaging system.

This conversion technique could be immensely useful for applications that require negative-time correlation, such as quantum-enhanced clock synchronization. Generating of negativetime correlation directly has some shortcomings compared with the conventional tried-and-true schemes that generate positivetime correlation. This technique could allow more flexibility in choosing two-photon sources for quantum optics applications. We can consider two photons in two optical modes, such as two polarization, two propagation directions, or two waveguide modes. The two-photon wave function is

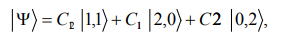
Where the constants C s are overall amplitudes of the quantum states, is the quantum state in which one photon is in each mode, is the state in which both photons are in mode 1 and is the state in which both photons are in mode 2. The positive-frequency forwardpropagating component of the electric field in each mode is given by

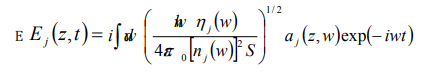
Where 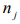is the complex, frequency-dependent refractive index in mode 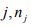, is the real part of 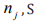, S is an area of quantization in the x-y plane, and 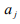is the photon annihilation operator, related to the corresponding creator operator via the equal-space commutator

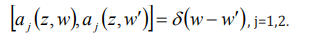
The physical significance of each amplitude 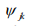is that its magnitude squared gives the probability density 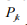of coincidentally measuring one photon in mode j at (z,t) and another photon in mode k at ,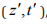

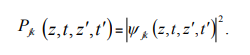
Plasmatic temporal entanglement is defined as irreducibility of into a product of one-photon amplitudes in the form of a(t)b( 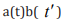). This means that the probability of detecting a photon in mode 1 at time t is correlated to the probability of detecting a photon in mode 2 at 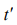. The most popular ways of generated entangled photons are spontaneous parametric down-conversion and four-wave mixing, where wave-mixing geometry and the spatiotemporal profile of the pump-beam determine the initial 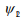. (17, 18)

The most interesting case is when M=-1 and one of the photons is time reversed. If the two photons are initially entangled with positive-time correlation 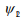can be written as 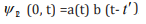, where b is assumed to be much sharper than a. After photon 1 has passed through the plasmatic temporal imaging system M=-1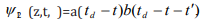 The photons hence become anticorrelated in time. Since most conventional two-photon sources generate positive-time correlation, but negative-time correlation is desirable for many applications, one can use the temporal imaging system to convert the former to the latter.

Besides the above application, one can also convert negativetime correlation, which can be generated by ultrashort pulses for improved efficiency, to positive correlation. Any desired correlation can actually be imposed on already entangled photons, by multiplying the original correlation with a factor of 1/M. As groupvelocity dispersion and temporal phase modulation play analogous roles in the time domain to diffraction and lenses, which can be use Fourier optics, temporal imaging, and quantum imaging techniques to design more complex quantum plasmatic temporal imaging systems. The quantum destructive interference via a coupler is determined by the overlap of the two photons amplitude with its plasmatic mirror image. The output amplitude is the destructive interference between the original amplitude and its replica but with the two photons exchanging their positions in time. In particular, for a 50%-50% coupler, T=R=1/2, complete destructive interference is produced if the two photons are temporarily indistinguishable. The introduction of variable distinguishability to photons, in order to produce varying degrees of destructive interference via a beam splitter to measure the two-coherence time, is the basic principle of the Hong-Ou-Mandel interferometer. As envisioned by Lukin and Imamoglu, the third-order nonlinear effects among two photons can become significant in a coherently prepared plasmatic atomic gas. The coupled-mode equations and then become nonlinear, where is the self-phase modulation coefficient and also cross-phase modulation coefficient. The advantage of the Schrödinger picture is most evident, whereas in the Heisenberg picture one needs to solve nonlinear coupled-mode operator equations, in the Schrödinger picture, one only needs to solve linear equations, which are similar to the configuration-space model applied to the quantum theory of solitons. The delta function couples the two subspaces, so entanglement can emerge from unentangled photons. A soliton formed by two photons in orthogonal polarizations exerting crossphase modulation on each other. Studies of two photons in the same mode under the self-phase modulation effect have been performed by entanglement, and cross-phase modulation offers the distinct possibility of entangling two photons in different modes.

Consider the case in which two polarizations have the same group-velocity dispersion, so that, and there is one photon in each polarization. The evolution equation for

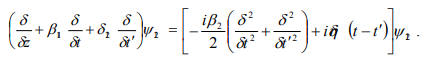
Defining time coordinates in a plasmatic moving frame.

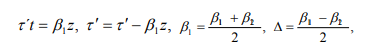
we obtain the following equation for :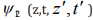

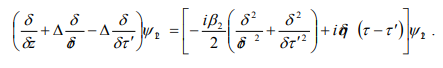
This equation is a simple linear Schrödinger equation, describing a two-dimensional “wave function” 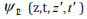in a moving frame subject to a 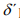potential. To solve for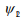

explicitly, we define new time coordinates

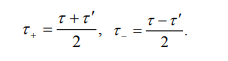
The cross-phase modulation effect only offers confinement of 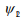along the time difference

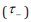axis, but not the mean arrival time 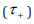axis. The only bound-state solution of 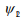is

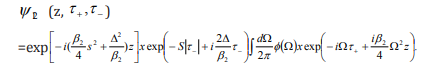
The delta potential enforces S to take on the valu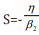e where 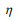and 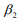must have opposite signs.

For 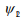the final solution in the plasmatic moving frame of 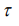and 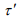is therefore

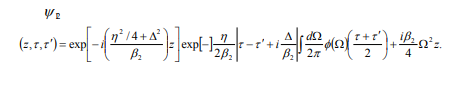
The two-photon coherence time of a vector soliton is fixed, but he average arrival time is still subject to dispersive spreading and becomes increasingly uncertain as they propagate. Hence a two-photon vector soliton generates temporal entanglement with positive-time correlation as it propagates. Similar to the idea of soliton momentum squeezing, one can also abiotically change along the propagation axis to control independently the two-photon coherence time. The center frequencies of the photons are shifted slightly, by an amount of to compensate for their group-velocity mismatch, so they can copropagating at average group velocity. This is commonly known as soliton trapping. If the nonlinearity has a finite bandwidth, the potential becomes a finite-bandwidth function and multiple bound-state solutions can be obtained via conventional techniques of solving the linear the Schrödinger equation.

We have derived the general equations that govern the temporal evolution of two-photon probability amplitudes in different coupled optical modes. The formalism inspires the concept of quantum temporal imaging, which can manipulate the temporal entanglement of photons via conventional imaging techniques. The theory also offers an intuitive interpretation of two-photon entanglement evolution, as demonstrated by the exact solution of the two-photon vector soliton. To conclude, we expect the proposed formalism to be useful for many Plasmatic Moving Frames, quantum signal processing and communication applications.

Plasma Medicine

Plasma sources used in plasma medicine are typically “low temperature” plasma sources operated at atmospheric pressure. In this context, low temperature refers to temperatures similar to room temperature, usually slightly above. There is a strict upper limit of 50°C when treating tissue to avoid burns. The plasmas are only partially ionized, with less than 1 ppm of the gas being charged species, and the rest composed of neutral gas.

a) Dielectric-barrier discharges

Dielectric-barrier discharges are a type of plasma source that limits the current using a dielectric that covers one or both electrodes. A conventional DBD device comprises two planar electrodes with at least one of them covered with a dielectric material and the electrodes are separated by a small gap which is called the discharge gap. DBDs are usually driven by high AC voltages with frequencies in the kHz range. In order to use DC and 50/60 Hz power sources investigators developed the Resistive Barrier Discharge (RBD) [3]. However, for medical application of DBD devices, the human body itself can serve as one of the two electrodes making it sufficient to devise plasma sources that consist of only one electrode covered with a dielectric such as alumina or quartz. DBD for medical applications [4] such as for the inactivation of bacteria, [5] for treatment of skin diseases and wounds, tumor treatment [6] and disinfection of skin surface are currently under investigation. The treatment usually takes place in the room air. They are generally powered by several kilovolt biases using either AC or pulsed power supplies.

b) Atmospheric Pressure Plasma Jets

Atmospheric pressure plasma jets (APPJs) are a collection of plasma sources that use a gas flow to deliver the reactive species generated in the plasma to the tissue or sample. The gas used is usually helium or argon, sometimes with a small amount (< 5%) of O2, H2O or N2 mixed in to increase the production of chemically reactive atoms and molecules. The use of a noble gas keeps temperatures low and makes it simpler to produce a stable discharge. The gas flow also serves to generate a region where room air is in contact with and diffusing into the noble gas, which is where much of the reactive species are produced [7]. There is a large variety in jet designs used in experiments [8]. Many APPJs use a dielectric to limit current, just like in a DBD, but not all do. Those that use a dielectric to limit current usually consists of a tube made of quartz or alumina, with a high voltage electrode wrapped around the outside. There can also be a grounded electrode wrapped around the outside of the dielectric tube. Designs that do not use a dielectric to limit the current use a high voltage pin electrode at the center of the quartz tube. These devices all generate ionization waves that begin inside the jet and propagate out to mix with the ambient air. Even though the plasma may look continuous, it is actually a series of ionization waves or “plasma bullets”.(8) This ionization wave may or may not treat the tissue being treated. Direct contact of the plasma with the tissue or sample can result in dramatically larger amounts of reactive species, charged species, and photons being delivered to the sample [9]. One type of design that does not use a dielectric to limit the current is two planar electrodes with a gas flow running between them. In this case, the plasma does not exit the jet, and only the neutral atoms and molecules and photons reach the sample. Most devices of this type produce thin (mm diameter) plasma jets, larger surfaces can be treated simultaneously by joining many such jets or by multielectrode systems. Significantly larger surfaces can be treated than with an individual jet. Further, the distance between the device and the skin is to a certain degree variable, as the skin is not needed as a plasma electrode, significantly simplifying use on the patient. Low temperature plasma jets have been used in various biomedical applications ranging from the inactivation of bacteria to the killing of cancer cells [10].

Applications

Plasma medicine can be subdivided into three main fields:

a) Non-thermal atmospheric-pressure direct plasma for medical therapy.

b) Plasma-assisted modification of bio-relevant surfaces.

c) Plasma-based bio-decontamination and sterilization.

Non-thermal atmospheric-pressure plasma

One of challenges is the application of non-thermal plasmas directly on the surface of human body or on internal organs. Whereas for surface modification and biological decontamination both low-pressure and atmospheric pressure plasmas can be used, for direct therapeutic applications only atmospheric pressure plasma sources are applicable. The high reactivity of plasma is a result of different plasma components: electromagnetic radiation (UV/VUV, visible light, IR, high-frequency electromagnetic fields, etc.) on the one hand and ions, electrons and reactive chemical species, primarily radicals, on the other. Besides surgical plasma application like argon plasma coagulation (APC), [11] which is based on high-intensity lethal plasma effects, first and sporadic non-thermal therapeutic plasma applications are documented in literature [12]. However, the basic understanding of mechanisms of plasma effects on different components of living systems is in the early beginning. Especially for the field of direct therapeutic plasma application, a fundamental knowledge of the mechanisms of plasma interaction with living cells and tissue is essential as a scientific basis.

Mechanisms

Though many positive results have been seen in the experiments, it is not clear what the dominant mechanism of action is for any applications in plasma medicine. The plasma treatment generates reactive oxygen and nitrogen species, which include free radicals. These species include O, O3 , OH, H2 O2 , HO2 , NO, ONOOH and many others. This increase the oxidative stress on cells, which may explain the selective killing of cancer cells, which are already oxidatively stressed [13]. Additionally, prokaryotic cells may be more sensitive to the oxidative stress than eukaryotic cells, allowing for selective killing of bacteria.

It is known that electric fields can influence cell membranes from studies on electroporation. Electric fields on the cells being treated by a plasma jet can be high enough to produce electroporation, which may directly influence the cell behavior, or may simply allow more reactive species to enter the cell. Both physical and chemical properties of plasma are known to induce uptake of nanomaterials in cells. For example, the uptake of 20 nm gold nanoparticles can be stimulated in cancer cells using non-lethal doses of cold plasma. Uptake mechanisms involve both energy dependent endocytosis and energy independent transport across cell membranes [14]. The role of the immune system in plasma medicine has recently become very convincing. It is possible that the reactive species introduced by a plasma recruit a systemic immune response [15].

Conclusion

For the first time ever, physicists have captured an image of quantum entanglement. In a paper published in the journal of Scientific Advances, scientists from the University of Glasglow shared the first known image of a Bell entanglement. The photo depicts two photons interacting and sharing physical states for a brief instant -- an event that occurs regardless of the actual distance between the particles [16]. To capture a picture of the Bell entanglement, physicists created a system that shoots off streams of entangled photons from a quantum source of light at what they call “non-conventional objects.” These objects are displayed on liquidcrystal materials, which can change the phase of the photons as they move through them. A camera capable of detecting photons was then set to snap a photo when it identified one photon entangled with another. According to the researchers, quantum entanglement is one of the primary pillars of quantum mechanics. The concept is used in practical applications like quantum computing and cryptography, but no one has ever managed to capture an image of it in action. Physicists involved in the project believe that the image can help to advance the field of quantum computing and lead to new types of imaging [16-19]. These results confirm our theory on the Plasmatic Moving Frames (PMF).

The Transfiguration

As he was praying, the appearance of Jesus’s face changed, and his clothes became as bright as a flash of lightning [20]. While he was speaking, a cloud appeared and enveloped them, and they were afraid as they entered the cloud. (35) A voice came from the cloud, saying, “This is my Son, whom I have chosen; listen to him. LUKE 9: 29-36 These possible transfigurations is part of the abovementioned new types of imaging, what explanation and proves our theory of Plasmatic Moving Frames in quantum physics and optics.

Read More Lupine Publishers Otolaryngology Journal Articles:
https://lupine-publishers-otolaryngology.blogspot.com/