Lupine Publishers| An Image Secret Sharing Method Based on Shamir Secret Sharing

 Lupine Publishers| Journal of Computer Science and Applications

Abstract

This paper presents an image secret sharing method based on Shamir secret sharing method. We use the matrix projection to construct secret sharing scheme. A secret image to be divided as n image shares such that:

i) Any k image shares (k ≤n) can be used to reconstruct the secret image in lossless manner and

ii) Any (k-1) or fewer image shares cannot get sufficient information too reveal the secret image.

It is an effective, reliable and secure method to prevent the secret image from being lost, stolen and corrupted. In comparison with other image secret sharing method this approach’s advantages are its strong protection of the secret image and its ability for real time processing.

Keywords: Image secret sharing; Finite field; Matrix projection

Introduction

The effective and secure protection for important message is a primary concern in commercial and military applications. Numerous techniques, such as image hiding and watermarking, were developed to increase the security of the secret. The secret image sharing approaches are useful for protecting sensitive information [1]. The main idea of secret sharing is to transform an image into n shadow images that are transmitted and stored separately. The original image can be reconstructed only if the shadow images that participated in the revealing process from a qualified set [2]. The (k; n)-threshold image sharing schemes were developed to avoid the single point failure. Hence the encoded content is corrupted during transmission. In these schemes, the original image can be revealed if k or more of these n shadow images are obtained. Moreover, the users who with complete knowledge of k 1 shares cannot obtain the original image. Blakley [3] & Shamir [4] independently proposed original concepts of secret sharing in 1979. In these (k; n)-threshold schemes encode the input data D into n shares, which are then distributed among k recipients. D can be reconstructed by anyone who obtains a predefined number k, where 1 k n, of the images.

Noar & Shamir [5,6] extended the secret sharing concept into image research and referred it as visual cryptography. Visual cryptography requires stacking any k image shares (or shadow images) to show the original image without any cryptographic computation. The disadvantages are

i) Image shares have larger image size compared to the size of the original secret image and

ii) The contrast ratio in the reconstructed image is quite poor [7].

A better image secret sharing approach was presented by Thien & Lin [1]. They used Shamir’s secret sharing scheme to share a secret image with some cryptographic computation. The method significantly reduces the size of the secret image and the secret image can be reconstructed with good quality. Ramp secret sharing schemes are another types of secret sharing schemes [8- 11]. In ramp schemes, a secret can be shared among a group of participants in such way that only sets of at least k participants can reconstruct the secret and k1 participants cannot [12]. The rest of this paper is organized as follows. Section II reviews the Shamir’s scheme. The proposed secret image sharing method and experimental results are given in Section III. It is also explained the advantages of proposed scheme in this section. The last section collects concluding remarks.

Review of shamir’s secret sharing scheme

Shamir [4] developed the idea of a (k, n)-threshold based secret sharing technique (k ≤n). The technique allows a polynomial function of order (k -1) constructed as,

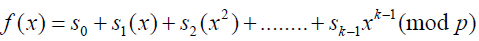, where the value of s0 is the secret and p is a prime number. The secret shares are the pairs of values (x_i, y_i) where, 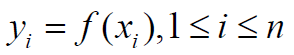and 0⩽𝓍₁1⩽𝓍₂⩽.........𝓍_n⩽p-1 The polynomial function f(x) is destroyed after each shareholder possesses a pair of values (xi, yi) so that no single shareholder knows the secret value s₀ [7]. Actually, no groups of (k 1) or fewer secret shares can discover the secret s₀. That is when k or more secret shares are available, then we may set at least k linear equations y_i = f(x_i) for the unknown s_i’s. The unique solution to these equations shows that the secret value s₀ can be easily obtained by using Lagrange interpolation [4].

Proposed Method

In this section, we examine the application of some secret sharing schemes. We have worked a new approach to construct secret sharing schemes based on field extensions in [13]. In this paper, we generalise the results of [13].

The application of some secret sharing schemes

Digital image consists of by transporting images in the nature through the agency of sensors to the computer. Digital images are sampled signals at regular intervals. These sampling points are called the pixel. The image is a two dimensional matrix which consists of pixels. It should be determined that how many bits of each pixel value will be stored when this matrix is constructed. This value is called the bit depth. For an image with a bit depth of 8, the maximum value that a pixel can have is 255. In general, it is used 3 bands to obtain a color picture. These bands have same size and each matrix represents a different color component. Each color component corresponds to red, green and blue.

Proposed scheme

Consider the matrix I is an image with height of h and wideness of w. The height corresponds to row number of matrix and the wideness corresponds to column number. Let the secret space be Mq for a pixel, where

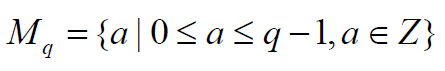. This set consists of the elements of the matrix I. Let the secret be the image I and the threshold structure be (k; n). In this case, it can be constructed a secret sharing scheme as follows.

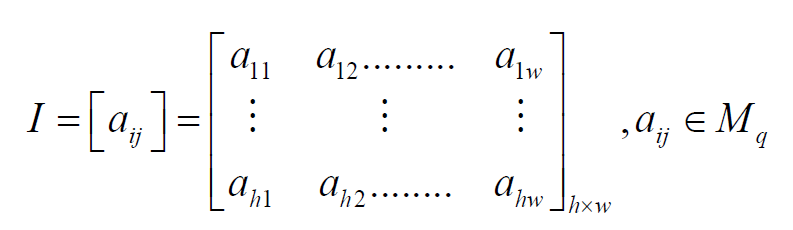
The matrix P(x) is generated which consisting of height of h and wideness of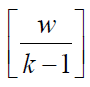 by using I.

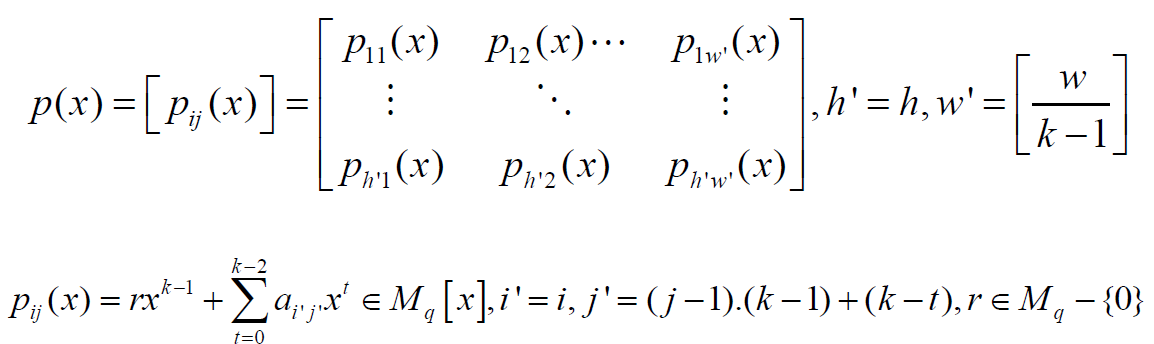
The a_ij entry corresponds to i th row and j th column of matrix I. It is clear that the degree of polynomial pij is (k -1). The columns of the matrix I are divided into pieces that has length of (k -1). j th piece in the i th row is represented by the vector H_ij = {h₁; h₁…. h_k-1}. It is used the vector H_ij to construct the element p_ij=1(1≤𝒾≤𝒽',1≤𝒿≤𝓌') of the matrix p(x). The first entry of H_ij is located i th row and [(j - 1) (k - 1) + 1] th column of the matrix I. The leading coefficient of polynomial p_ij(x) is randomly chosen from Mq – {0}. The coefficient of term which is the degree of t = (0 ≤ t ≤ k − 2) of polynomial p_ij(x) is chosen as (k - t -1) th element of H_ij. This corresponds to [(j - 1) (k - 1) + (k - t)] th column in the i^th row. The matrix P(x) is written as the elements of matrix T(x) by using Algorithm 1 [13].

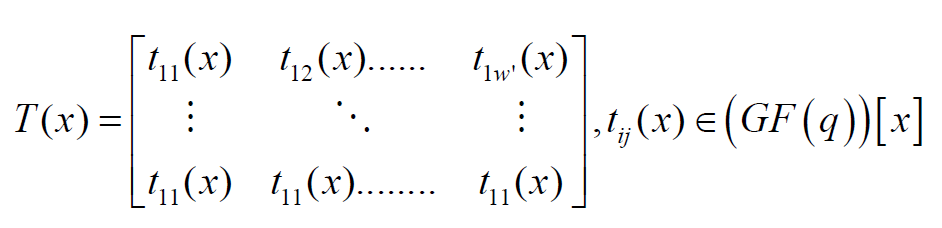
It is determined an ID number for each participant. The secret piece is obtained by equality (5) for each participant and 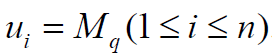These ID numbers are transformed to the.

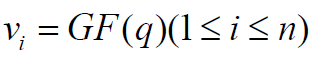by Algorithm 1 [13]. Then the matrix 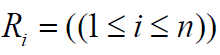is transformed to the matrix T(x) as follows.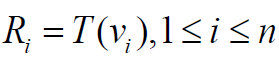

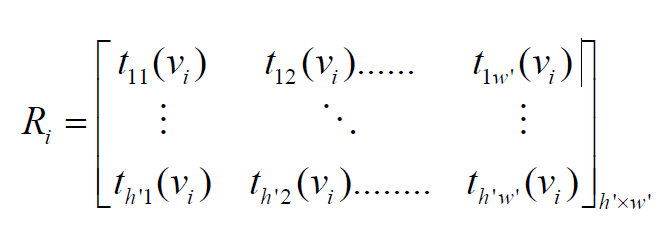
This polynomial matrix is written as the matrix Yi by using Algorithm 2 [5].

Secret retrieval procedure

To reach the secret, at least k pieces of secret must be known. On the other hand, the number of elements of 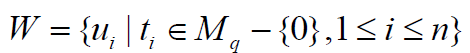must be at least k. In the ordered pair (𝓊_ti; Y_𝓊ti) the ordered of participant in the W is denoted by i, the order of the set of participant of t_i th participant in the W is denoted by 𝓊_ti. Y_𝓊ti is the secret piece which is given to participant with ID of 𝓊_ti. These ordered pairs are transformed to the ordered pairs (𝒱_ti;R_𝓊ti) i ti t u v R by using algorithm 1 in [13]. It is used to Lagrange Interpolation for the ordered pairs ( ; ) i ti t u v R . Hence it is obtained the matrix T(x) again. Then it is found the matrix P(x). The image is constructed with the coefficients of this polynomial.

Example. Let the secret space be M256 and the irreducible polynomial be f(x) = x⁸ + x⁴ + x³ + x² +1∈(GF(2))[x] to construct GF (256). It can be constructed a (3; 5)-threshold schemes by using the following matrix I.

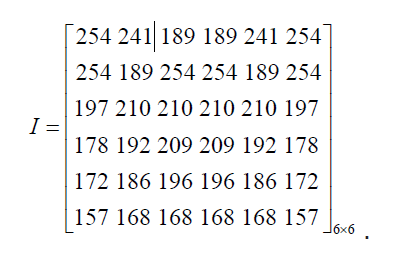
The matrix P(x) can be constructed as follows. The leading coefficient is randomly selected and the other coefficients are chosen from matrix I.

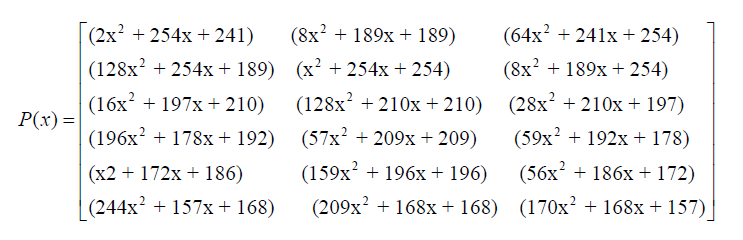
The coefficient of polynomial in the matrix P(x) is moved to GF(256). Therefore, it is obtained the elements of matrix T(x) = [tij(x)]; (t(x) 2 (GF(q))[x]).

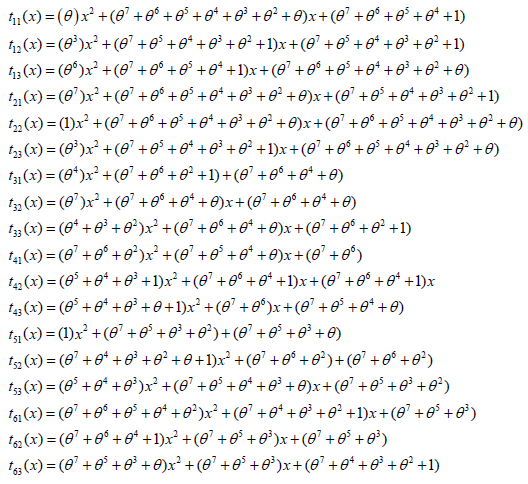
Let the IDs of participants be 𝒰₁ = 1, 𝒰₂ = 2, 𝒰₃ = 3, 𝒰₄ = 4 and 𝒰₅ = 5. These elements correspond to 2 𝒱₁ =1,𝒱₂ =θ ,𝒱₃ =θ +1,𝒱₄ =θ₂ and 𝒱₅ =θ +1∈GF(256)

The pieces of participants are as follows.

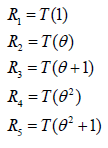
These elements correspond to the following matrices in M256.

At least 3 participants can recover the image by combining their shares by using Lagrange Interpolation in [13]. It is seen that the original secret image in Figure (1a) and the secret pieces are seen (1b-1d). Reconstructed image is seen in Figure (1f).

Advantages

It is known that a file in the computer environment can be expressed with a bit string. A bit string consists of 8 bits is called a byte. A byte gets value in the range (0-255) and is an element of M256. A file D consisting of m bytes can be expressed as a vector such that D = (a₁ a₂……… am) (a_i∈M_q) . Consider any file (text, image, video, etc.) by using the proposed scheme, the file is also secret. The operations an secret sharing schemes can be applied to this file. The participants know that the secret is the image. The secret sharing scheme is defined over GF(256). So it is a lossless scheme. As in the Shamir’s scheme if the operations were done in GF(251), then the large values of 250 would be lost. That is the file will be corrupted. So, the entire file could be lost. At result the image could not reconstruct again.

Conclusion

We proposed an image secret sharing method based on Shamir secret sharing. We have two techniques. i) Secret sharing scheme using matrix projection and ii) Shamir’s secret sharing scheme. A secret image can be successfully reconstructed from any k image shares but cannot be revealed from any (k-1) or fewer image shares. The size of image shares is smaller than the size of the secret image. Our scheme is defined over GF(256). So it is a lossless scheme. This is another advantage of our scheme. So the proposed scheme stands well, in terms of security.

Read More About Lupine Publisher Journal of Computer Science and Applications Please Click on Below Link:
https://computer-sciences-lupine-publishers.blogspot.com/