Lupine Publishers| Journal of Biostatistics & Biometrics
Abstract
This paper proposes a generalization of the length biased exponential distribution, called the Gompertz length biased exponential (GLBE) distribution. Some of the basic properties of the proposed model were derived in minute details and model parameters estimated by the maximum likelihood estimate method. The adequacy of the model is empirically validated with the use of real - life data.
Keywords: Exponential Distribution; Length Biased; Gompertz Generalized Family Of Distribution; Quantile Function; Hazard Functions; Survival Function
Introduction
Length biased distributions are special case of the more general form known as weighted distribution [1], first introduced by [2] to model ascertainment bias and formalized in a unifying theory by [3]. Lifetime data may be modeled with several existing distributions, although the existing models are not adequate or are less representative of actual data in many situations. Therefore, the development of compound distributions that could better describe certain phenomena and make them more flexible than the baseline distribution is of great importance [4]. Thus, the choice of the model is also an important issue for reliable model parameter estimation. Some exponential distribution generalizations for modeling lifetime data due to some interesting advantages have been recently proposed [5]. In recent years many exponential distribution generalizations have been developed, such as the Marshall Olkin length biased exponential distribution [5], exponentiated exponential [6,7], generalized exponentiated moment exponential [8], extended exponentiated exponential [19], Marshall-Olkin exponential Weibull [10], Marshall-Olkin generalized exponential [5], and exponentiated moment exponential [11] distributions.
A random variable X is said to have a length biased exponential distribution with parameter \beta if its probability density function (pdf) and cumulative distribution function (cdf) is given by equation (1) and (2) respectively [12]:
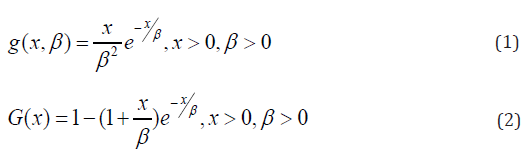
Where is the scale parameter.
The survival function is given by the equation
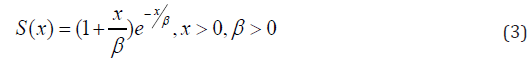
The hazard function is
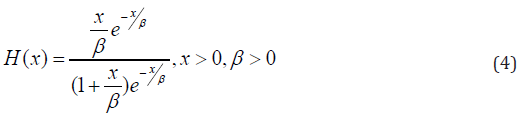
And the reversed hazard rate function is
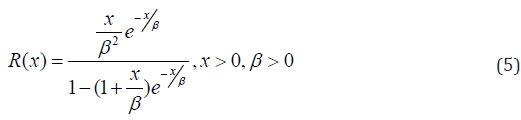
Alzaatreh et al. [13] defined the cumulative distribution function of the Transformed-Transformer (T-X) family of distributions by;
And the corresponding probability density function by;
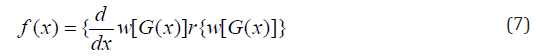
Morad Alizadeh et al [14] defined the cumulative distribution function and probability density function of the Gompertz Generalized family of distribution by setting
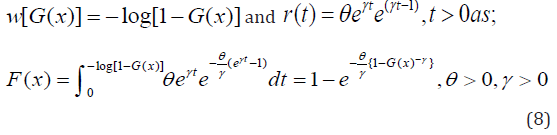
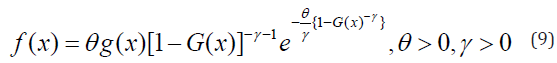
respectively. Where \theta and \gamma are additional shape parameters whose role is to vary the tail length.
Thus, we proposed a new generalization of the length biased exponential distribution called the Gompertz length biased exponential (Go-LBE) distribution. In the rest of the paper, we define the Go-LBE model and plots for different parameter values in Section 2; some of the statistical properties of the proposed Go-LBE distribution are discussed in minute details in section 3, Application of the Go-LBE distribution to a lifetime data in section 4. The concluding remark is presented in section 5.
Gompertz Length Biased Exponential (Go-LBE) Distribution
The cumulative distribution function of the
Figure 1: Graph for Go-LBE cumulative distribution function at different parameter values.
Figure 2: Graph for Go-LBE probability density function at different parameter values.
Figure 3: Graph for Go-LBE survival function at different parameter values.
Figure 4: Graph for Go-LBE hazard function at different parameter values.
Figure 5: Histogram of the fitted distributions.
Figure 6: Empirical cdf of the fitted distributions.
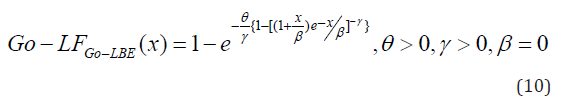
Some Statistical Properties of the Go-LBE Distribution
Basic properties such as the asymptotic behavior, parameter estimation and order statistics of the Go-LBE distribution are discussed in minute details.
Asymptotic Behavior
Here we critically examine the behavior of the Go-LBE model in equation (11) as x→0 and as x→∞
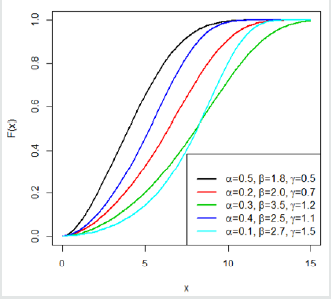
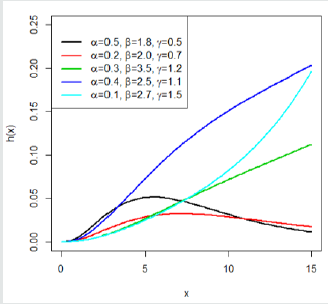
This indicates that the Gompertz length biased exponential distribution is unimodal. A clear observation of Figure 2 shows the Go-LBE model has only one peak. This supports our claim that the Go-LBE distribution has only one mode.
Parameter Estimation
Using maximum likelihood estimation techniques, we estimate the unknown parameter of the Go-LBE model based on a complete sample. Let X...Xn indicate a random sample of the complete Go-LBE distribution data, and then the sample’s likelihood function is given as;
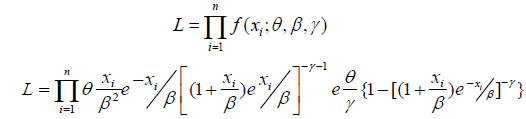
We can now express the log likelihood function as;
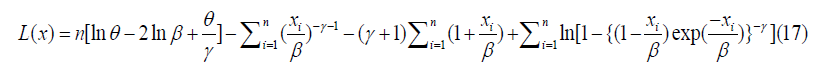
By taking the derivative with respect toθ ,γ andβ , and fixing the outcome to zero, we have;
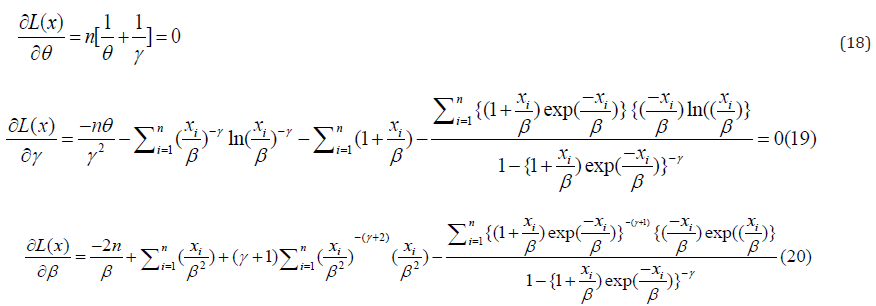
Solving equation (18)-(20) iteratively, will give the estimate of the parameters of the Go-LBE model.
Order Statistics
We considered a random sample denoted by from the densities of the Go-LBE distribution. Then,
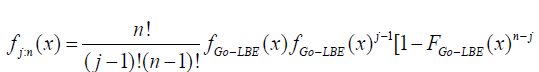
The probability density function of the order statistics for the Go-LBE distribution is given as;
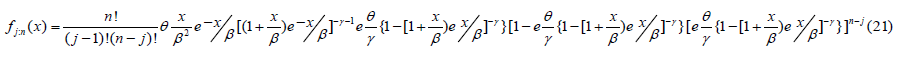
The Go-LBE distribution has minimum order statistics given as;
Data Analysis
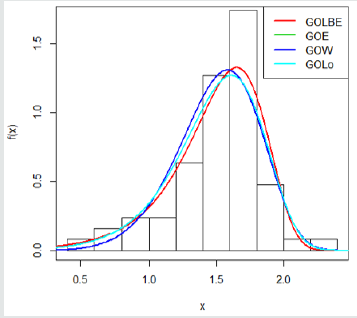
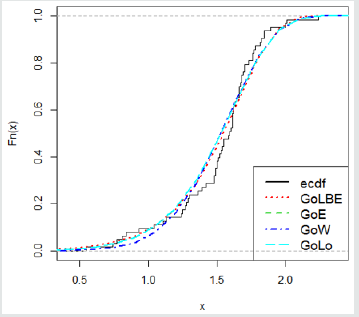
Here, we provide an application of the Gompertz length biased exponential distribution by comparing the results of the model fit with that of other Gompertz- G family of distributions. The data set we employ is the uncensored strength of 1.5cm glass fibre data previously used by Bourguignon M et al. [15], Merovci F et al. [16]. This data set will be used to compare between fits of the Gompertz length biased exponential distribution (Go-LBE) with that of Gompertz-Exponential (Go-E), Gompertz-Lomax (Go-L), and, Gompertz-Weibull (Go-W). The data is presented below (Tables 1 & 2):
Table 1: Descriptive Statistics on Cancer Stem Cell Data.
Table 2: MLEs, SW, AD and K–S of parameters for Cancer Stem Cell data.
0.55, 0.74, 0.77, 0.81, 0.84, 1.24, 0.93, 1.04, 1.11, 1.13, 1.30, 1.25, 1.27, 1.28, 1.29, 1.48, 1.36, 1.39, 1.42, 1.48, 1.51, 1.49, 1.49, 1.50, 1.50, 1.55, 1.52, 1.53, 1.54, 1.55, 1.61, 1.58, 1.59, 1.60, 1.61, 1.63, 1.61, 1.61, 1.62, 1.62, 1.67, 1.64, 1.66, 1.66, 1.66, 1.70, 1.68, 1.68, 1.69, 1.70, 1.78, 1.73, 1.76, 1.76, 1.77, 1.89, 1.81, 1.82, 1.84, 1.84, 2.00, 2.01, 2.24
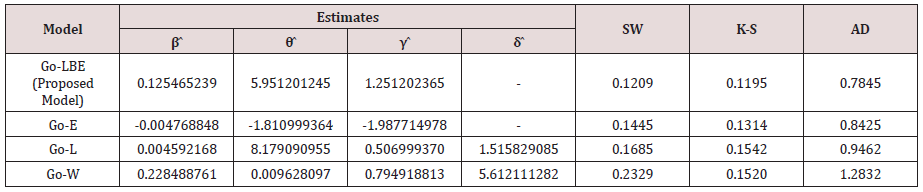
For all competing distributions using the strength of glass fibre data set, Table 2 shows parameter estimate and the value for the Shapiro Wilk (S-W), Anderson Darling (AD), and the Kolmogorov Smirnov (K-S) statistic (Table 3).
From Table 3, the Go-LBE has the highest log-likelihood values and the lowest AIC, CAIC, BIC and HQIC values; hence, it is chosen as the most appropriate model amongst the considered distributions.
Table 3: Log-likelihood, AIC, AICC, BIC and HQIC values of models fitted for Cancer Stem Cell data.
Conclusion
This research has successfully extended the length biased exponential distribution. Densities and basic statistical expressions were briefly derived. The performance of the proposed Gompertz length biased exponential distribution was compared to existing models in literature based on the negative log likelihood, AIC, CAIC, BIC and HQIC values. Based on the lowest criterion values, we therefore conclude that the Gompertz length biased exponential distribution is the most suitable model amongst the considered models and indeed a very competent model for describing life-time situations.
Read More About Lupine Publishers Journal of Biostatistics & Biometrics Please Click on Below Link: https://lupine-publishers-biostatistics.blogspot.com/
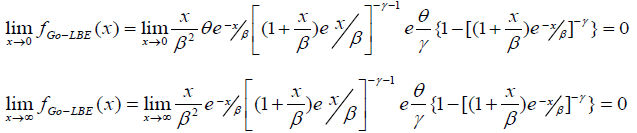
No comments:
Post a Comment
Note: only a member of this blog may post a comment.