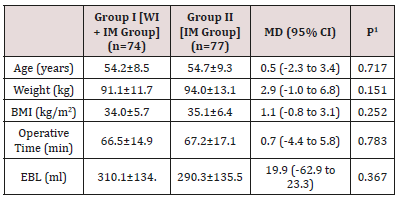
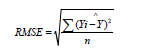Yield predictions allow for decision making regarding management of
agricultural yield before and after harvest by government
and decision-makers. Traditional approaches to collect yield statistics
such as manual field surveys and physical computation of
yield are costly and take a long time for information to be available.
Remote sensing platforms such as hyperspectral data provide
real-time, fast, and reliable statistics that can be used to derive
yield information. Vegetation indices are ratios used to combine
multiple band observations of the hyperspectral data into one index and
applied to derive soybean grain yield. The objective of this
study was to evaluate the potential of vegetation indices derived from
hyperspectral data to predict soybean grain yield. Soybean
hyperspectral data was acquired using a handheld spectroradiometer with a
spectral range of 350 to 2500 nm in March and April of
the summer season of 2017. The random forest regression algorithm was
used to predict the soybean grain yield. NDVI, SR and EVI
were calculated from the hyperspectral data for all probable bands
situated in the 400 nm and 2399 regions. The results showed
that relevant wavelengths in predicting soybean were combinations
situated in the red-edge (680-750 nm), NIR and the MIR (1300
to 2399 nm) of the electromagnetic spectrum. Furthermore, regression
results showed that SR better predicted the soybean grain
yield (R2
= 0.843) compared to NDVI (R2
= 0.841) and EVI (R2
= 0.537). In overall, the results of this study suggest that narrow-band
indices have the potential to predict soybean grain yield.
Keywords: Soybean Yield; Hyperspectral Data; Vegetation Indices
Abbreviations: NDVI: Normalised Difference Vegetation Index; SR: Simple Ratio; EVI: Enhanced Vegetation Index; RF: Random
Forest; RMSE: Root Mean Square Error; FS: Free State; MP: Mpumalanga
Introduction
South Africa is the third dominant consumer of soybean in the
world [1]. Mpumalanga, KwaZulu Natal and Free State provinces
are the largest soybean producers in the country [2]. Over the last
decade, soybean production and consumption in South Africa has
increased [1,3]. Currently, soybean production does not meet South
African local demands [3]. As a result, South Africa imports large
quantities of soybean products [3]. Attaining higher yields entails
increasing the area planted and/or use of more fertilisers [4].
Production in both approaches requires constant crop monitoring
using reliable techniques that can provide real-time statistics.
Constant monitoring of crops can enhance chances of attaining
higher yield through early detection of problems that can potentially
affect yield. Soybean yield information in the hands of farmers
and policy makers is important for decisions such as planning for
harvesting, yield management and market related decisions [5].
Thus, there is a need for an efficient real-time monitoring system to
provide the status, growth and development of soybean information
consistently that can enable yield predictions.
Various methods have been used to predict grain crop yields
and these include the use of agricultural censuses, field surveys [6]
and physical computation of yields by visiting numerous sample
areas [7]. In South Africa, current yield predictions are based
upon field surveys conducted telephonically, via emails, and or by
post FAO [8]. However prediction methods based on traditional
crop yields surveys are frequently subjective, susceptible to large
inaccuracies and take a long time for information to be available for
the benefit of food security and early planning before and during
harvests [5]. In addition, yield predictions obtained influence
the pricing of agricultural commodities and the decisions to be
taken regarding imports and exports [8]. This therefore validates
the need for crop monitoring initiatives that involve the use of
reliable techniques such as remote sensing to ensure fair pricing
of agricultural commodities and objective decision-making. Remote
sensing methods are suitable; they include the acquisition of crop
canopy measurements [9], and can deliver immediate, reliable,
measurable evaluations of the ability of plants to capture radiation
and photosynthesize [10]. These canopy spectral measurements
are beneficial for estimating crop yield [9]. Research shows that
remote sensing spectral bands have strong relationships with
vegetation biomass [11].
Many researchers have used broadband multispectral data to
predict yield of various crops such as maize [12], rice [5], soybean
[10] and wheat [13,14]. Broadband multispectral data have
advantages as it is applicable to regional areas and also because
of numerous revisits of the same area as well as capturing data
at large spatial scales in real-time [15]. In addition, multispectral
data is available at low or no cost, which can be beneficial to
countries with limited resources [15]. Despite these advantages,
broadband data has drawbacks for vegetation observation such
as exhibiting excessive spectral differences and shadows due to
the above-ground coverage and landscape [11]. The latter can be a
hindrance in producing precise biomass prediction models with the
ability to distinguish between soil background and vegetation [11].
Precise biomass predictions are essential for effective monitoring
and management of vegetation [11]. Furthermore, broadband
data does not have specific narrow-bands that precisely focus on
biochemical and biophysical factors of crops [16,17]. This suggests
that multispectral broadband data exhibit difficulties in monitoring
crops with high biomass such as soybean. Although
multispectral broadband data have these disadvantages, research
has shown that these disadvantages can be overcome by the use
of vegetation indices [18]. Vegetation indices eliminate differences
caused by soil background, above-ground geometry, sun view
angles as well as the influence of atmospheric circumstances
when assessing biophysical characteristics of vegetation at aboveground
scale [18]. Widely used vegetation indices for vegetation
monitoring and modelling are calculated using the red and the near
infrared (NIR) bands [19]. The red and NIR bands respond to the
biochemical and biophysical properties of crops [16,19]. These
spectral bands are sensitive to the rate of photosynthetic activity
in green vegetation [20]. The Normalised Difference Vegetation
Index (NDVI) [21] and Simple Ratio (SR) [22] are commonly
utilised indices that are calculated using the NIR and the red bands
[20] with applications for crop monitoring. Soybean has been
monitored using NDVI modelled from broadband data sets such
as AVHRR/NOAA [23,24] and ADAR 5500 4 band digital camera
with a broadband width of 450 nm to 90 nm [25]. [26] used SR,
NDVI, Soil Adjusted Vegetation Index (SAVI) and Transformed SAVI
(TSAVI) to evaluate soybean biophysical properties such as yield,
photosynthetically active radiation (PAR), leaf area index (LAI) and
biomass [26]. Also, the SR index is known to be able to decrease
the effect of soil background on the spectral reflectance and is also
sensitive to changes occurring at prime developmental phases of
vegetation [27]. The Enhanced Vegetation Index (EVI) is another
widely used vegetation index in agricultural forecasting computed
using the red and NIR bands with an addition of the blue band [28].
However, the EVI is insensitive to saturation when faced with high
biomass vegetation [29]. Despite the usefulness of these spectral
bands, broadband data is unresponsive to the variation in plant
features [15].
Due to disadvantages encountered by broadband data,
researchers promote the use of hyperspectral data that covers the
whole range of the electromagnetic spectrum instead of just two
or three bands [18]. Hyperspectral data provide advantages of
handiness, flexibility, controllability and high temporal resolution,
which are greatly beneficial in precision agriculture applications as
opposed to satellite based platforms [30]. Also, hyperspectral data
contains other important spectral bands such as the red edge bands
that are useful in the study of vegetation [18]. The red edge band
is highly responsive to variations in biomass of green vegetation
[18]. Narrow bands are important for supplying more information
with substantial enhancements compared to broad bands in
enumerating biophysical properties of agricultural crops [17,31].
Also, hyperspectral data is important for modelling yield features of
agricultural crops [17] such as chlorophyll content, photosynthetic
activities and leaf structure [32]. Numerous researchers have used
hyperspectral data for vegetation monitoring such as [17,18,31]
with positive results. Mutanga and Skidmore [18] calculated NDVI
from hyperspectral data and obtained that regular NDVI including
strong chlorophyll absorption bands in the red region and NIR
region inadequately predicted biomass (R2
=0.26). Whereas, the
modified NDVI (MNDVI) that included bands in the range (700-
750 nm) and narrow-bands in the red-edge region (750-780 nm)
showed a high predictive ability for biomass (R2
=0.77). Mariotto et
al. [18] identified that important bands when modelling biophysical
properties of maize, wheat, cotton, rice and alfafa, (about 74%
of them) are situated in the 1051-2331 nm regions. The remaining
30% of these bands are in the 970 nm region (10%), red-edge region
(6%) and the visible region (10%) (Blue region (400-500nm), green
region (501-600 nm) and NIR region (760-900 nm). Thenkabail et al. [31]
concluded that stronger correlations with crop biophysical
characteristics were situated in the red region (650-700 nm),
shorter wavelengths of the green region (500-550 nm), the NIR
region (900-940nm) and in the moisture sensitive area centred at
982 nm. Similarly, many researchers have used hyperspectral data
to predict yield of agricultural crops such as lint [33], wheat [34],
maize [35] and soybean [21]. However, for soybean [21] utilised
spectral data acquired using a multispectral hand-held radiometer
with a fewer number of bands. They obtained positive correlation
between NDVI and soybean grain yield (R2
= 0.80). Research has
shown that hyperspectral data has enabled estimation of yield of
various crops and biomass of several vegetation types. However,
soybean grain yield has not been predicted comprehensively using
hyperspectral data in the spectral range of 400-2399 nm.
Hyperspectral data has however some limitations, such as
those related to high dimensionality and redundancy [36] and the
problem of multicollinearity [37]. As a result, identifying suitable
bands for modelling is a challenging process. To overcome this
problem researchers encourage the use of advanced statistical
methods such as random forest (RF) regression algorithm [11].
Random forest is a regression algorithm that applies bootstrapping
aggregation to create a group of trees based on the randomness
of samples taken from the training data [38]. The random forest
algorithm is known to be able to handle the high dimensionality
of hyperspectral data and reduce data redundancy [37]. Also,
random forest has been noted to perform better than other
machine learning algorithms such as support vector machine and
neural network because of its robustness against overfitting [11,
38-41]. The aim of this study was to evaluate the performance of
narrow-band vegetation indices NDVI, SR and EVI derived from
hyperspectral data in predicting soybean grain yield. The vegetation
indices selected for the study are those frequently used for biomass
or agricultural crop and ecological vegetation studies [18] and
have been applied successfully in predicting other crops. The main
objective of this study is to assess the relationships of narrow-band
NDVI, SR and EVI to soybean grain yield. The second objective was
to identify suitable narrow-band indices to predict soybean grain
yield. The third objective was to compare the performance of NDVI,
SR and EVI random forest models developed from narrow bands
(400 nm to 2399 nm) in predicting soybean grain yield.
Materials and Methods
Study Sites
The research was conducted on two experimental farms
located in the Free State Province of South Africa in Phuthaditjhaba
(28°25’26”S and 28°56’12”E) and in the Mpumalanga province in
Ermelo (26° 45’18” S and 30° 13’55” E) (Figure 1). The Free State
and Mpumalanga provinces experience warm summers with high
rainfall and cold winters. Both these areas receive approximately
625 mm of precipitation annually with most precipitation
occurring in summer (October - March). The soil in Phuthaditjhaba
can be characterised as “rich loam” type of soil [42] while the soil
in Ermelo can be characterised as “low clay” [43] and sandy soil.
Figure 1: Map showing the location of the study sites in Free State (FS) and Mpumalanga (MP) provinces.

Experimental Setup
The experiment on both sites followed a split plot Randomized
Complete Block Design (RCBD) method. In the two study sites, 72
experimental plots each with a size of 7 m length and 3 m width
were used. The plots consisted of 7 rows with 60 cm row spacing.
Three soybean cultivars from Pannar seeds (PANN 1500 R, PANN
1614 R and PANN 1664 R) were sown from the 13th to 15th December
2016 in the MP and from 19th to 21st of December 2016 in FS site.
Fertilizer treatments of 0 kg, 30 kg and 60 kg of phosphorus (P)
were applied to the plots to provide more nutrients and enhance
the health of the soybean plants. The experiment consisted of three
replicates and the soybean relied on rainwater for irrigation.
Field Spectral Measurements
The first set of field spectral measurements in Mpumalanga and
Free State were taken in March 2017 and the second set of spectral
measurements were taken in April 2017. During this period, the
soybean had reached maximum canopy cover whereby the soil
background could have little effect on the spectral measurements.
Due to differences in planting date, the soybean in Mpumalanga
was in the pod formation stage during the first visit while in the
Free State site it was still flowering. Canopy spectral measurements
were acquired during flowering, pod formation and seed filling
stages randomly plot by plot across fertilizer treatments of 0 kg,
30 kg and 60 kg. An Analytical Spectral Device (ASD) Field Spec®3
optical sensor (Analytical Spectral Devices, Inc., Boulder, CO, USA)
was used to take spectral measurements from 10:00 am to 14:00
pm local time (GMT+2). The spectroradiometer records wavelength
ranging from 350 to 2500 nm, measuring radiation at 1.4 nm
bandwidths for the spectral region of 350-1000 nm and registers
2 nm intervals for the spectral region of 1001-2500 nm [44]. The
spectral measurements
were taken under cloud free conditions. In each plot, 5 spectral
measurements were taken with the optical cable connected to the
spectroradiometer held at about 30 cm above the soybean canopy.
Every 10 to 15 minutes a white reference spectralon calibration
panel was used to balance any changes in the atmosphere and
irradiance of the sun. The spectral measurements were added
together to obtain the medial spectral measurements for each plot.
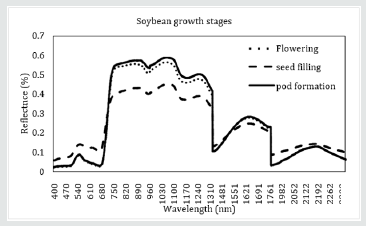
Figure 2 shows average spectral reflectance of soybean at flowering,
pod formation and seed filling stages. The spectral reflectance
curve indicates the amount of radiation absorbed and reflected by
the soybean at different regions of the spectrum. For soybean, the
flowering and pod formation stages are critical stages in which the
soybean utilises the absorbed radiation to photosynthesise and
form grains [45]. A higher spectral signature is an indicator of a
healthy crop in which higher yield can be expected whereas a low
spectral signature indicates a lower yield [45].
Figure 2: Average spectral curves of soybean canopies at flowering, pod formation and seed filling stages.
Soybean Yield Data
To obtain soybean grain yield data, the soybean pods were
harvested from the middle 3 rows of each plot at the end of the
growing season of May and June 2017. The soybean pods were then
crushed to obtain the soybean grains. The soybean grains obtained
from each plot were weighed using the LBK1 weighing scale from
ADAM Equipment [46]. The grains measurements of specific plots
for each site were added to obtain the total yield of the soybean of
each site.
Data analysiss
448 Bands allocated from 350 to 399 nm, 1350 to 1450 nm,
1800 to 1950 nm and 2400 to 2500 nm were omitted from the
analysis due to atmospheric water absorption and the effect of noise
in the reflectance spectra following techniques outlined in [11,36].
The remaining 1702 narrow-bands situated between 400 nm and
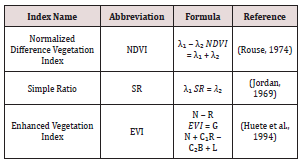
2399 nm were used to compute the narrow-band indices.The NDVI,
SR and EVI indices were calculated using the standard indices
equations [22, 28,47] (Table 1). These indices were calculated
from all probable two-bands combinations including 1702 narrow
bands situated between 400 and 2399 nm [11,18,19]. The narrow
bands are presented as λ₁ (400-2399 nm) and λ₂ (400-2399 nm)
combinations following approaches outlined in [18]. The calculated
vegetation indices were correlated to the soybean yield using the
Spearman’s correlation coefficient [2]. The correlations between
vegetation indices and soybean grain yield were calculated to
assess their relationship.
Table 1: Vegetation indices computed from the λ1 (400-2399 nm)
and λ2 (400-2399 nm) combinations.
Assessing the Differences in Yields between Study Sites
and Fertilizer Treatments
Exploratory data analysis was performed to understand the data
before any statistical analysis was done. The statistical analysis was
performed in STATISTICA 13 software testing for normalcy of the
data using Lilliefors test [48]. Furthermore, an analysis of variance
was performed to determine if there were differences in soybean
grain yield means between the two study sites and between the
three fertilizer treatments.
Statistical Analysis Using the Random forest (RF)
Regression
The random forest regression technique was used to predict
the soybean grain yield. RF is a machine learning algorithm
developed by Breiman [49] that applies a bootstrap aggregation
method in which an ensemble of trees (ntree) are developed on
the basis of the randomness of samples extracted from the training
data. For regression, the random forest permits trees to grow to the
highest magnitude without trimming, depending on the bootstrap
sample from the training data [49]. At every tree, the RF grows a
randomized subgroup of predictors (mtry) to identify the optimum
split at every node of the tree [41]. At the end, the RF averages the
outcome of the overall sum of trees in order to obtain the overall
estimation [50]. From the bootstrap samples of the training data
(2/3), each tree grows randomly and selected independently. The
residual original data (1/3) of the excluded samples (called outof-bag (OOB)) are then used to validate the model and predict
variables of importance [51,52].
RF requires two parameters to be tuned that are (i) (ntree) the
number of trees to grow and (ii) (mtry) the number of variables
that are split at each node [41]. The ntree and the mtry parameters
(vegetation indices) were then optimized for the random forest
model using the top 20 NDVI, SR and EVI data sets to determine the
best index that can be used to predict soybean grain yield. The mtry
was calculated for all probable band combinations while the ntree
was evaluated at 500, 1000, 1500, 2000, 2500, 3000, 3500, 4000,
4500, and 5000 trees. The random forest model was developed
from 70% (2/3) of the training data to build a model that can predict
soybean grain yield (g/m2
) and 30% (1/3) of the test data was
used to validate the model (OOB). Important indices at predicting
soybean grain yield were selected by the RF using the permutation
variable importance measures (mean decrease in accuracy). The RF
algorithm was implemented using the R statistical software using
the random Forest built in package to predict the soybean grain
yield (Liaw and Wiener, 2002).
Variable Importance Selection
Random forest calculates variable importance using the Gini
index and the permutation variable importance measures [53].
The permutation variable importance measure is defined as the
variation between the OOB error from the data set acquired by
random selection of the predictor variables and the OOB error
from the original data set [53]. While the Gini index variable
importance is a measure used in a classification when growing
trees in the random forest [54]. The permutation variable
importance measure is the most preferred measure of importance
as it assesses importance of variables using the mean decrease in
accuracy in the OOB predictions as forests are being assembled
[53]. Permutation variable importance predicts the importance of
a variable by determining how much prediction error rises when a
variable is selected while others remain the same [55,56]. For this
study, the permutation variable importance was used to determine
the combination of indices that were powerful than the others
in predicting soybean grain yield. From the ranking of the mean
decrease in accuracy, the top 3 important combinations of indices
were selected.
Accuracy Assessment
When using the random forest, research has shown that
there is no need for a different test data for validation because
the random forest uses an OOB error prediction built internally
[37,38,50,57,58]. This is particularly remarkable in situations
where data acquisition is highly dependent on oscillating weather
conditions. The random forest computes the OOB error as a result
of variance between the estimation made using the training
data set and the OOB data set [41,59]. OOB error produces an
unbiased evaluation of the prediction accuracy of the model [40].
The coefficient of determination (R2
) and root mean square error
(RMSE) were reported on the assessment of the accuracy of the
random forest models. RMSE was calculated using the formula
below:
where Ŷ and Y are measured and predicted soybean grain yield
respectively.
Results
Assessing the Differences in Soybean Yields between
Study Sites and Fertilizer Treatments
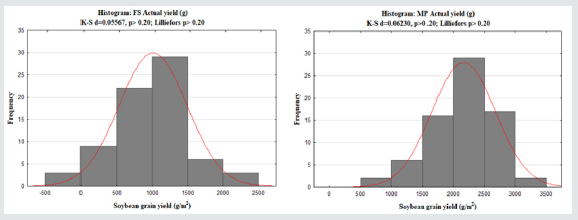
Exploratory statistics showed that soybean grain yield data
does not significantly deviate away from a normal distribution for
both sites (Figure 3) and thus meets the assumptions of ANOVA.
Analysis of variance results showed that there were significant
differences between the soybean grain yield in Free State and
Figure 3: Descriptive statistics of soybean grain yields for FS (a) and MP (b) sites.
Mpumalanga provinces (p≤0.05). However, the results showed
no significant differences in soybean grain yield between fertilizer
treatments on the study sites (p≥0.05). The total soybean grain
yield obtained in FS was 72816 g/m2
with an average of 1011.3 g/m2
per field while the total soybean grain yield in MP was 156060
g/m2
with an average of 2167.5 g/m2 per field. In total, the soybean
grain yield of both sites was 228876 g/m2 with an average of 1589.4
g/m2.
Narrow-Band NDVI and SR Relationship to Soybean Grain Yield
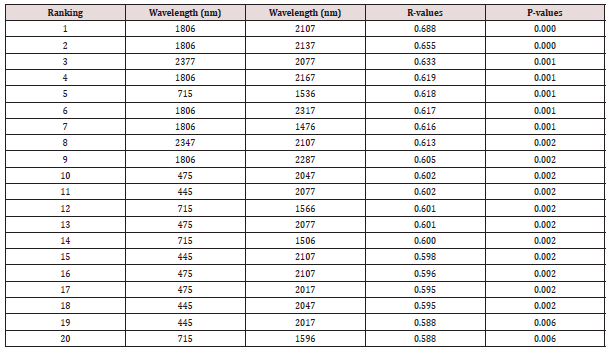
Table 2: Top 20 narrow band NDVI indices (λ=30 nm) that produced the highest correlation coefficients with soybean grain yield.
Narrow-band NDVI and SR were computed for all probable
two-band combinations in the spectral range 400 nm to 2399 nm.
Spearman’s correlation coefficients were applied to assess the
relationships of the narrow-band NDVI and SR to soybean yields.
The NDVI and SR obtained identical results of the correlations to
the soybean grain yield (Tables 2 & 3). The correlation coefficients
(R) results obtained between NDVI/SR and soybean grain yield
ranged from 0.00 to 0.68 shown in Tables 2 & 3.
Table 3: Top 20 narrow band SR indices (λ=30 nm) that produced the highest correlation coefficients with soybean grain yield.
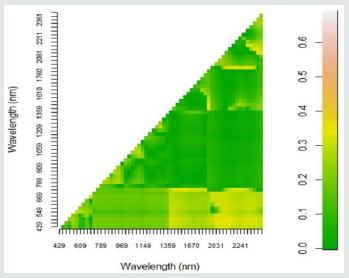
Figures 4 & 5 depict a graphical presentation of the R-values
for the relationship between soybean grain yield and NDVI and
SR. These results show a moderate to strong relationship between
NDVI/SR and the soybean grain yield (R-values from 0.588 to
0.688). In addition, the p-vales obtained for these results indicate
that the relationships between soybean grain yield and the
derived vegetation indices are significant as they are less that 0.05.
Correlation coefficients of NDVI and SR were arranged in the order
of the highest to the lowest and the top 20 R-values. The top 20 best
NDVI/SR indices are situated in the blue (445 nm - 475 nm), rededge (715 nm) and in the MIR regions (1506 nm – 2377 nm) of the
electromagnetic spectrum (Figures 4 & 5).
Figure 4: Heat map showing the correlation coefficients (R) between soybean grain yield and narrow band NDV acquired from
all probable band combinations from the spectral range of 400 nm to 2399 nm.
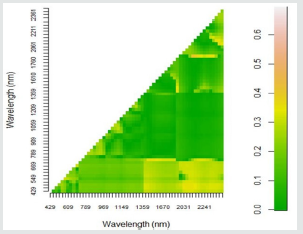
Figure 5: Heat map showing the correlation coefficients (R) between soybean grain yield and narrow band SR acquired from
all probable band combinations from the spectral range of 400 nm to 2399 nm.
Narrow-Band EVI Relationship to Soybean Grain Yield
Narrow-band EVI was computed from all probable band
combinations in the spectral range of 400 to 2399 nm of the
electromagnetic spectrum. Spearman’s correlation coefficients
were calculated to assess the relationship between the EVI indices
and the soybean grain yields. The correlation coefficient results
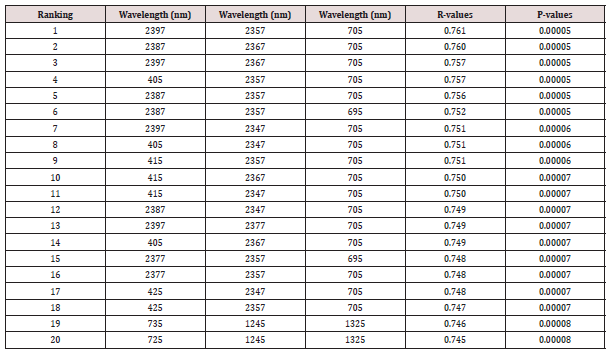
of EVI indices ranged from 0.00 and 0.761. The relationship
between soybean grain yield and the derived narrow- band EVI
are significant as shown by the p-values less than 0.05 in Table 4.
Correlation coefficients of the narrow-band EVI were ranked from
the highest to the lowest and the top 20 best indices were selected
and shown in Table 4. The best 20 EVIs are situated in the blue
region (405 nm – 425 nm), red region (695 nm), red-edge ((705
nm- 735 nm) NIR (1245 nm) and the MIR (2357 nm– 2397 nm)
regions of the electromagnetic spectrum.
Table 4: Top 20 narrow-band EVI indices (λ= 10 nm) that produced the highest correlation coefficients with soybean grain yield.
Optimization of the Random Forest Regression Models
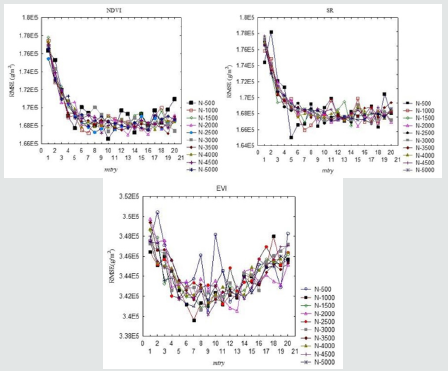
For the three indices (NDVI, SR and EVI), the ntree and mtry
values were optimized using the training dataset to identify values
that best predicted soybean grain yield. For each index, ntree values
from 500 to 5000 were tested and mtry was tested from 1 to 20
(Figure 6). The mtry and ntree values that produced the best RMSE
were selected. According to the results (Figure 2), the best mtry for
the NDVI and SR models were 10 and 5 and their ntree was 500
respectively. For EVI, the best mtry was 7 and the ntree was 1000.
Figure 6: Optimization of random forest parameters (ntree (N) and mtry) using RMSE.
Variable Importance of Narrow-Band Indices in
Predicting Soybean Grain Yield Using the RF
From the best 20 selected indices that were highly correlated
with the soybean grain yield, it was essential to categorize narrowband
indices of NDVI, SR and EVI that would highly perform when
predicting soybean grain yield (g/m2
). The RF calculated variable
importance using the mean decrease in accuracy to measure the
importance of NDVI, SR and EVI at predicting soybean grain yield
(g/m2
). The RF algorithm was capable of ranking the NDVI (Figure
7a), SR (Figure 7b) and EVI (Figure 7c) indices according to their
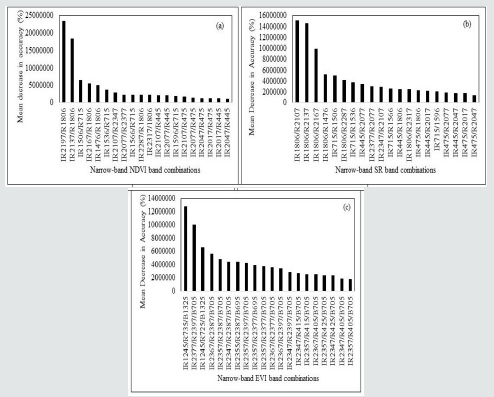
importance in predicting soybean grain yield.
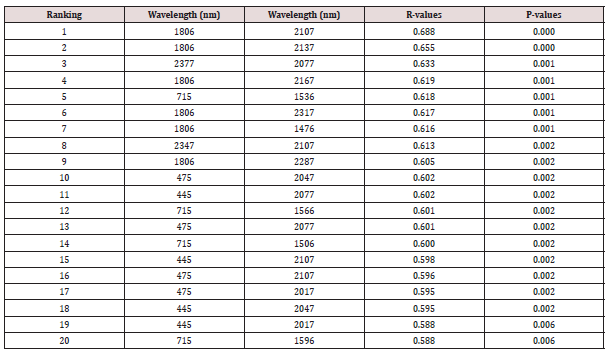
Using the mean decrease in accuracy arrangement, top 3
wavelength combinations that had significant importance in
predicting the soybean grain yield were selected. For NDVI, top 3
band combinations included:
(i) 2197 nm and 1806 nm,
(ii) 2137 nm and 1806 nm and
(iii) 1506 nm and 715 nm. similarly,
SR top 3 important wavelength combinations include
(i) 1806 nm and 2107 nm,
(ii) 1806 nm and 2137 nm and
(iii) 1806 nm and 2167 nm. In addition,
EVI top three significant wavelengths included
(i) 1245 nm, 735 nm and 1325 nm,
(ii) 2377 nm, 2397 nm and 705 nm and
(iii) 1245 nm, 725 nm and 1325 nm.
Figure 7: Mean Decrease in Accuracy (%) of NDVI (a), SR (b) and EVI (c) concluded by the random forest algorithm. Important
variables ranked are those with the highest mean decrease accuracy.
Accuracy Assessment
Figure 8: Random Forest models (NDVI (a), SR (b) and EVI (c)) showing sensitivity of ntree to the OOB error.
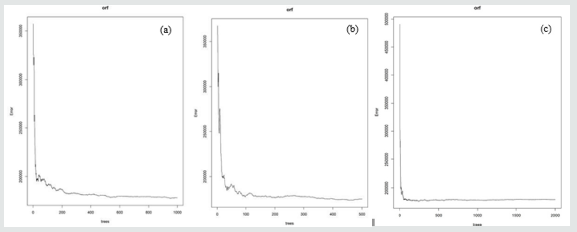
Figure 8 shows the best ntree results of the RF models for
NDVI (a), SR (b) and EVI (c). This indicates that for NDVI and
SR, the models obtained accuracy at 500 trees and at 1000 trees
for EVI. The coefficient of determination (R2
) and Root Mean
Square Error (RMSE) were statistical measures that were used to
evaluate the predictive performance and accuracy of the random
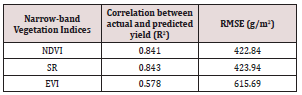
forest regression models (NDVI, SR and EVI). Table 5, shows the
performance results of the random forest prediction models. The results show that SR obtained the highest R2
of 0.843 with a RMSE
of SR= 423.94 and RMSE of NDVI=422.84 (26.11% of the average
soybean grain yield) compared to NDVI that obtained R2
=0.841
with an RMSE of 423.94 (26.04% of the average soybean grain
yield) and EVI (R2
= 0.578) (37.04% of the average soybean grain
yield) and RMSE of 615.94. These results suggest that SR can better
predict soybean, however NDVI obtained better accuracy in the
prediction in comparison to SR and EVI.
Table 5: Predictive performance of the NDVI, SR and EVI
random forest prediction models using top 20 best indices.
Discussion
The aim of the study was to evaluate the potential of narrowband indices (NDVI, SR and EVI) in predicting soybean grain yield
(g/m2
). Broadly, the results of this study demonstrated that narrowband situated in the blue, red, red edge and MIR regions have a
potential to predict soybean grain yield. The objectives were to
assess the relationships of the narrow-band indices to the soybean
grain yield, identify suitable narrow- band indices to predict
soybean and to compare the accuracy of the prediction models. The
study further showed that important bands in predicting soybean
grain yield are not only bands in the NIR and red regions but also
bands situated in the MIR region.
Assessment of the Relationships of Narrow-Band Indices
to Soybean Grain Yield
The R-values obtained for NDVI (0.00-0.688), SR (0.00-0.688)
and EVI (0.00-0.761) showed that different combinations of
bands respond differently to variations in soybean grain yield.
As shown in Tables 2-4, strong correlations to the soybean grain
yield did not only consist of combinations of bands in the red
and NIR regions. Strongly correlated indices of NDVI, SR and EVI
to soybean consisted of combinations of bands in the blue region
(405 nm - 475 nm), red region (695 nm), red edge (705-735 nm),
NIR (1245 nm) and the MIR regions (1325 nm -2397 nm). These
results correspond with those reported by Mutanga and Skidmore
[18], which suggested that information on vegetation biomass is
not only limited in the red and NIR bands. As a result, NDVI, SR and
EVI highest correlations mainly consisted of combinations of bands
in the MIR (1300-2399 nm) and combinations of the blue (400-
500 nm) bands and red-edge (700-729 nm) bands. The MIR region
is known to be sensitive to water content of leaves and has low
reflectance [32]. However, for this study, most MIR bands showed
strong sensitivity to biochemical factors found in soybean such as
nitrogen, protein as well as oil [32]. Similarly, wavelengths in the
blue region are highly sensitive to chlorophyll a and b since plants
absorb the violet-blue light for photosynthesis [32]. Based on
these results it is understandable that combinations of these bands
would obtain the highest correlation to the soybean grain yield.
These results also concur with those reported by Darvishzadeh et
al. [60,17]. Darvishzadeh et al. [60], showed that bands in the MIR
had the strongest relationship to leaf area index (LAI) compared
to the red and NIR bands. Mariotto et al. [17], reported that about
74% of bands sensitive to biophysical properties were situated
in the MIR (1051 to 2331 nm). Additionally, the red-edge band is
characterised by high reflectance and is linked to differences in the
chlorophyll content that is associated with biomass of vegetation
[18,32]. It is reasonable that combinations of wavelengths including
the red- edge would obtain a strong relationship to soybean grain
yield. Generally, these results provided more understanding of
the relationship of the soybean grain yield and its significant
wavelength regions. Furthermore, the results showed that
important information on soybean yield is mostly contained in the
MIR (1300 to 2399 nm) and indicate that narrow-bands have the
potential to predict soybean grain yield.
Variable Importance and Assessment of the Predictive
Performance of the NDVI, SR and EVI Random Forest
Models
In the top 20 selected indices that had a strong relationship
to soybean grain yield, it was necessary to identify which of those
were significant in the prediction of soybean grain yield. The
random forest used the mean decrease in accuracy measures to
identify combinations of bands that are most significant in the
prediction of soybean grain yield. The results of the optimization
of the random forest showed that 10, 5, and 7 indices (NDVI, SR
and EVI) out of 20 indices (predictors) at 500 and 1000 ntrees
were significant at predicting soybean grain yield. These results
further demonstrated that accuracy of the prediction was obtained
with a smaller number of trees (ntree=500) compared to a larger
number of trees (ntree = 1000). These results were validated by the
differences in RMSE of 423.94 at 500 ntree compared to the RMSE
= 615.69 at 1000 ntree. The obtained results concur with those of
Abdel-Rahman et al. [41] who suggested that fewer number of trees
(ntree) results in lower RMSE, which indicates better accuracy. The
R2
results of the NDVI, SR and EVI random forest models showed
that SR obtained the highest R2
in predicting soybean grain yield.
These results indicate that, compared to the NDVI and EVI, SR is
a better index at predicting soybean grain yield. These findings
are similar to those obtained by Mutanga and Skidmore [18] who
in their study concluded that SR (R2
=0.80) was a better index at
predicting biomass in dense canopies than NDVI and Transformed
Vegetation Index (TVI). Higher performance of SR could be because
of its high sensitivity to high biomass as compared to NDVI which
saturates when faced with high biomass [61,62]. Although the SR
obtained the highest R2
, the NDVI obtained the lowest RMSE of 422.84 compared to SR (RMSE=423.94) and EVI (RMSE=615.69).
These findings indicate that NDVI has better accuracy at predicting
soybean yield since a lower RMSE indicates better accuracy. In
conclusion, these results suggest that both the SR and NDVI can
accurately predict soybean grain yield.
Conclusion
This study shows the success of narrow-band indices in
predicting soybean grain yield. The results have shown that
important narrow-bands in predicting soybean grain yield are not
only combinations of bands situated in the red (695 nm) and the
NIR (1245 nm) regions but are also combinations of bands found in
the blue region (405 nm - 475 nm), red edge (705 nm -735 nm) and
the MIR regions (1325 nm -2397) nm. Furthermore, the SR index
(R2
= 0.843) proved to be a better index in predicting soybean grain
yield compared to the NDVI (R2
= 0.841) and EVI (R2
= 0.578).
Acknowledgement
We acknowledge the Agricultural Research Council (ARC),
the National Research Foundation (NRF) and the University of
the Free State for the financial support for this study. We thank
the Soil Science division in ARC that allowed us to collect soybean
reflectance data from their experimental farms. Thank you to
Dr Solomon Newete and Eric Economon for their assistance in
acquiring spectral reflectance data.
Read More About Lupine Publishers Journal of Environmental & Soil Sciences Please Click on Below Link:
https://lupine-environmental-soil-sciences.blogspot.com/